首页 -> 2007年第2期

小学数学教学中基于“问题情境”的建模范式解读

作者：朱旭平　徐旭琴

　　新课改实施过程是新旧教学观念、教学方式方法激烈碰撞的过程，其中对数学与生活的关系是普遍存在而一直没有得到妥善解决的一个问题：一方面在小学数学教学中，我们反对纯数学和纯生活两种方式的教学，那如何辩证地、和谐地结合数学与生活呢?即如何从生活现象中抽取出数学问题，提炼出数学模型，再应用数学模型解决生活问题；另一方面在课堂教学中如何具体操作，如何引领学生思维从具体到抽象再到具体，学生语言从生活语言向数学语言过渡。为解决此问题及有机融合新旧教学观念、思想和行为而开展本课题研究。本课题清晰地阐述数学课堂教学从“问题情景(原型)——数学建模——应用解模”的循环往复的一个过程，明确了一个基本观点：数学是模型的科学，建模是构建数学与生活的桥梁，形成了基于“问题情景”的建模教学范式，重点研究了建模思想在课堂教学中的尝试应用，具体阐述了教学范式理论与实践两个层面的链接——教学理论与教学流程、教学策略与典型案例等等。
　　
　　一、建模思想在课堂教学的应用尝试
　　
　　我们认为：建模的过程就是实际问题数学化的过程(见图1)。
　　
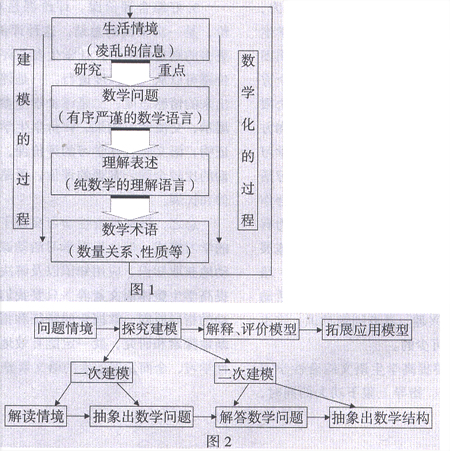
　　1．一次建模。从生活情境中抽象出数学问题，这是生活数学向学校数学的抽象，这个抽象出来的数学问题就是数模，如图表、应用题等。它经历了对情景问题中蕴含的数学成分进行分析和描述的过程，经历了从一些属于学生的、不那么正规的数学语言通过简化和形式化不断地向比较严格和正规的语言靠拢的过程。
　　2．二次建模。探究抽象出来的数学问题，再从数学问题中抽象出纯数学的理解表述(即意义理解，解题思路和策略)或数学术语(即数量关系、性质、法则等方法或概念)，这两者也是数模。
　　3．模型的建构程度。概念方法等数学术语模型的构建并不是一步到位的，因为从知识的发展角度来看，情景问题不是孤立地、重复的而是以滚动式的集束出现，这样学生未曾接触过的新概念、新思想、新方法会不断涌现，一些类似的事情反复出现，某些思路和方法会多次重复，循着这样的途径，一些学生先前并不知晓的概念和方法不断成型。这个过程不是一蹴而就的，需要花费一些工夫，但最终一个严格的数学系统会被重新发现和建构起来。
　　
　　二、基于“问题情景”的建模教学范式
　　
　　基于“问题情景”的建模教学范式(具体教学流程见图2)强调学生在一定的情景中学习，激发学生头脑中原有的生活经验，也容易使他们用积累的经验来感受其中所蕴含的数学信息，通过对各种信息的分析，从中发现数学问题，建立起符合学生自己经验的认知结构。
　　1．预设问题情景、感知数学模型。“不能追求完美而忽视数学，不能追求数学而牵强符会”，这是情景创设的原则。情景是为数学服务的，它不是摆设，也不是为了赶时髦的点缀品，不能求一时热闹好玩，而让数学成为情景的附属品。在情景创设时应注意以下三个方面：(1)情景内容的合理性。要适合学生的特点，符合生活实际的事理，更要符合数学的特征，蕴含着数学的信息，同时要注意把握在情景中知识和生活两方面融合的“度”，两者不能处于分离或勉强合成的状态，要能够以自然的方式隐含着学习中所要解决的数学问题；(2)情景的针对性。要和教学内容直接产生联系，尤其和重难点知识紧密结合，要为一定的教学目标服务的，在后面的教学中发挥一定的导向作用；(3)情景的开放性和模糊性。要留出让学生自己补充、收集信息的余地，可用信息和最终结论更有待学生自己去挖掘、去抽象。
　　2．合作探究、构建数学模型。(1)一次建模——解读问题情景，抽象成数学问题。教师引领学生解读、分析生活情景，激活学生已有的生活经验，并利用学生已有生活经验来感受、发现、提出其中所蕴含的数学问题，从而建构新的认知结构。在这个过程中，学生提出的数学问题并不是一步到位的，这需要教师有机地进行引导。若没有相应地进行指导与引导，那么情境活动则会变为支离破碎的学生经验，因为并非所有的学生经验都有同等的教育价值，有些经验不在弄清它们之间相互联系的基础上组织起来，它们在教学方面就要起消极作用。在引导时主要采取两种方法：一是针对情景“以问引问”，使情景和数学问题有机的整合起来，提高学生的提问能力；二是呈现多个情景有序地推进数学问题的深入。
　　案例1：面积和面积单位
　　1．问题情境。老师家要搞装修，买来了两种装修的材料，一种是长长的木条，一种是大大的三合板(电脑呈现：木条和木板的图)，你知道它们分别用在哪里吗?
　　2．抽取概念。根据学生的回答抽象出概念的表象，木条用于组成框架，它的长短就是物体的周长；木板用于面上，它的大小就是物体的面积。(板书见图3)
　　【思考】数学概念的建立需要表象作支撑，创设装修生活情境，通过教师提问：“你们知道。在装修中长长的木条和大大的木板分别用在哪里?”学生的回答就还原了周长、面积在生活中的原型，在两者表象对比抽取的过程中，经历了从问题情境——抽取概念的过程，加深了对概念的理解。
　　(2)二次建模——探索数学问题，抽象出数学结构。对小学生来说，在教师引导下从具体的生活情境中发现一些数学问题是学习数学的重要阶段，但这并不是数学学习的全部。只有让学生对发现的问题进行概括整理，从中寻找其普通的规律，并能抽象出数学结构(即数学模型)，如：应用题的数量关系、公式、性质、法则等，这样学生才能进入到一个较理性思考问题阶段。在组织学生对数学问题进行探索时，有时让学生独立探索，有时让学生协作学习，有时是独立探索和协作学习相结合，要根据数学问题的难易程度，灵活选择探索方法，达到数学建模的目的。
　　案例2：面积和面积单位
　　1．猜想面积单位。问题：我们用怎样的标准来规定(教具为1平方分米)呢?学生可能呈现两种链接：①已有知识联想，已经学习过长度单位：厘米、分米、米，猜想以边长为1厘米、1分米、1米的正方形为标准，或根据已有知识估计教具边长为1分米的正方形；②已有生活经验链接，学生在生活中接触的面积单位最多是平方米，再根据教具正方形联想到平方分米和平方厘米。
　　2．同桌合作、图象构建。各画出边长是1厘米和边长是1分米的正方形，并剪出来，用绳摆或米尺表示出边长是1米的正方形。呈现后师指出这些正方形的面积大小就分别是1平方厘米、1平方分米、1平方米，我们把它们称为面积单位。
　　【思考】根据三个面积单位的并列关系，对三个面积单位采用整体推进的方式教学，学生根据已有的知识(已掌握1厘米、1分米、1米等长度单位等)和生活经验，猜想面积单位教学，通过合作操作构建出面积单位的具体表象，从而达到数学建模的目的，使学生经历从模糊到清晰的过程，比较准确地感受到三个面积单位的

1 [2]