首页 -> 2007年第7期
我国宏观特殊教育系统的系统动力学研究
作者:石学云 高 丽
关键字系统动力学 宏观特殊教育系统 模型
分类号 G760
1 问题的提出
查有梁先生在认知心理学、中国古代的阴阳五行学说以及系统科学原理的启示下,提出用“五个指标”来研究宏观教育系统,这五个指标分别是:按人口平均的国民收入〔a〕;按人口平均每年的教育经费〔b〕;平均每万人口的教师人数〔c〕;平均每万人口的在校学生人数〔d〕;平均每万人口的文化程度分布〔e〕。进一步分析,上述的五个指标之间具有“相生”的关系,即按人口平均的国民收入决定了按人口平均每年的教育经费,〔a〕生〔b〕;教育经费供养着各类教师,即〔b〕生〔c〕;各级各类的教师培养着各级各类的学生,可以说〔c〕生〔d〕;在校学生一经毕业就直接影响着每万人口的文化程度分布,可以说〔d〕生〔e〕;而每万人口的文化程度分布直接制约着按人口平均的国民收入,即〔e〕生〔a〕。所以它们之间的关系就可以表示成为:
〔a〕→〔b〕→〔c〕→〔d〕→〔e〕→[1]
↑ │
┕┉┉┉┉┉┉┉┉┉┉┉┉┉┚
这种分析方式为我国宏观特殊教育系统的研究工作提供了一个全新的视角。结合系统动力学的相关理论和方法,我们可以对我国宏观特殊教育系统的内部结构及其相互关系加以分析,进而通过系统仿真,模拟预测未来我国在一定的特殊教育投资方式和经济发展水平下特殊教育的发展状况,从而为政策制定者提供必要的理论参考。
按照系统动力学的观点,这五个指标之间的相生关系可以被看作是因果关系。而这种相生关系是否真的存在,与现实是否相符,考虑到回归检验可以检验出不同因素之间是否存在因果关系,可以利用现有的相关数据,对其两两进行回归分析。在具体收集数据的过程中,考虑到数据的全面性和收集数据的可操作性,同时也为了使指标更加准确地反映现实中的问题,更加简单且能够最大程度地代表指标其本身,并结合我国宏观特殊教育的特点,我们对这五个指标做了一些调整和取舍:将按人口平均的国民生产总值(即人均GNP)调整为按人口平均的国内生产总值(即人均GDP)〔at〕,主要考虑的因素是历年人均GDP可以比较方便地从各类年鉴中收集到,并且GDP和GNP之间的换算关系很简单,在许多现实应用中,一个的变化能比较敏锐地反映出另一个的变化。将按人口平均每年的教育经费转变为生均特殊教育经费,即用每年国家对特殊学校的所有投资总和除以该年特殊学校的在校学生总数,主要考虑的是特殊人口的数据收集上存在困难,目前可以参考的残疾人口数量只有少量年限的抽样数据,其他各年的数据都只能根据实际人口数量和残疾人口的比例来估计,所以可能会存在比较大的误差;同时,生均特殊教育经费指标本身也能比较准确地反映国家对特殊教育的重视程度以及特殊教育本身的发展趋势,该指标记为bt。将平均每万人口的教师数调整为特殊教育专任教师数〔ct〕。这里的改变比较多,首先是将教师数改为专任教师数,其中主要考虑教师数除了包括专任教师外,还有其他的教辅人员,而我国从1997年开始就开始精简机构,教辅人员的数量在一定程度上受到控制,从而会影响教师整体数量的提高。其次直接使用了专任教师的绝对数量,而不是每万人拥有的专任教师量,主要考虑特殊教育中专任教师的绝对数量本身不大,而且,如果仿照原来的将每万人调整为每万特殊人口,数量收集中也存在困难。基于与ct同样的考虑,将平均每万人口的在校学生数调整为特殊教育学校的在校学生数〔dt〕。对于每万人口的文化程度分布的这个指标,这里直接用的是每年的特殊教育学校毕业生数量〔et〕,它最能代表我国特殊儿童的受教育水平。
综合上面的调整结果,借用查有梁先生的相生理论,调整后新的五个指标之间的关系也可以表示为:
〔at〕→〔bt〕→〔ct〕→〔dt〕→〔et〕→
↑ │
┕┉┉┉┉┉┉┉┉┉┉┉┉┉┉┉┚
2 回归检验及结果分析
2.1 相关数据
根据中国教育统计年鉴(2004)[2]和中国统计年鉴数据(1997-2002,2005)[3],我们整理出1996年至2000年历年人均GDP、特殊教育生均教育经费、特殊教育专任教师数、特殊教育在校学生数和特殊教育毕业生数各项指标数据,见表1:
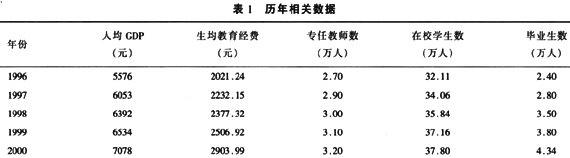
2.2 人均GDP〔at〕与生均年教育经费〔bt〕的回归分析
比较各种曲线回归的效果,可以看出二次曲线回归的拟合度最好,整理回归结果可以得到下表:
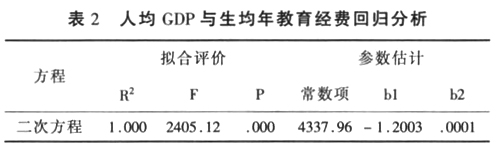
在以at为自变量、bt为因变量建立方程,决定系数R2=1.000,作拟合优度检验,方差分析表明:F=2405.12,P=0.000,拟合度很好,二次方程为:bt=4337.96-1.2003at+0.0001at2。
从回归结果也可以看出,人口平均的国内生产总值GDP〔at〕与生均年教育经费〔bt〕之间关系。根据统计结果可以很明确地看出,这二者之间存在明显的因果关系,随着人均GDP的提高,特殊教育在校生的人均年教育经费也提高,后者提高的速度甚至要大于前者。
2.3 生均年教育经费〔bt〕与特殊教育专任教师数〔ct〕的回归分析
这组关系的回归分析中,二次曲线和三次曲线的拟合程度都算是比较好的,二者的差别不大,二次拟合的效果稍微好一点,整理如下表:
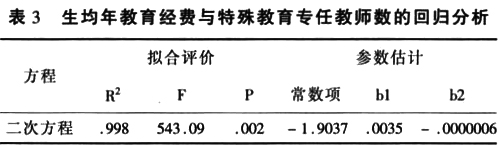
这里以二次曲线为例,以bt为自变量,ct为因变量建立方程,决定系数R2=0.998,作拟合优度检验,方差分析表明:F=543.09,P=0.002,拟合度较好,二次方程为:ct=-1.9037+0.0035bt-0.0000006bt2。
从回归结果可以看出,按人口平均的年教育经费〔bt〕与平均每万受教育人口的专任教师数〔ct〕二者之间也存在比较强的因果关系,但是观测点相对的分布比较零散(特别是与第一组数据:人均GDP与人均教育经费的关系相比),这也可以从一定程度上认为是二者的因果关系没有前一组强。查有梁先生在考虑二者的相生关系时,出发点是随着人均年教育经费的增加,可以供养更多的教师,从而按人口平均的教师的数量应当是增加的。从统计结果看,似乎也可以这样解释。但我们认为,统计图中观察点之所以显得比较凌乱,还应考虑到生师比提高的问题。生师比提高,势必会使教师人数的增长受到遏制,所以与普通教育一样,特殊教育中专任教师数随着人均年教育经费的增长会受到一定的遏制。
2.4 特殊教育专任教师数〔ct〕与特殊教育在校学生数〔dt〕的回归分析
这组数据的因果关系是比较明显的,但拟合程度没有前面的两组好,如下表:

以ct为自变量,dt为因变量建立方程,决定系数R2=0.984,作拟合优度检验,方差分析表明:F=61.5,P=0.016,拟合度一般,二次方程为:dt=-7.3407+16.7492ct-0.8056ct2。