|
视觉组织不同方面的相互依存性。三维组织:网膜像差;不同“深度标准”的结合;空间的方向错误。可见运动:可见运动理论的一般原理;断续运动和实际运动;似动速度:布朗实验;布朗的结果和柯特定律;运动和时间;融合的选择。关于行为物体之性质的结论。小结。
视觉组织不同方面的相互依存性
传统上,从形状恒常性、大小恒常性和颜色恒常性(包括透明度恒常性)的观点出发来进行的现象讨论,应当已经证明了对于知觉的理解(nuderstanding
of
perception)具有根本重要性的一般事实:我们的视觉世界的不同方面,包括大小、形状、颜色、方向(orientation)和定位(localization),都是由彻底的相互依存性(interdependence)所组成的。心理学在开始处理知觉问题时,还没有认识到该任务的复杂性。据认为,视觉世界的不同方面有其不同的和独立的根源,它们可以分别加以研究。起初,一种色觉和一种空间感觉得到区分,嗣后又补充了一种形状感觉,甚至可能还有运动感觉。由于将不同的问题转化成不同的现实,这样一种观点发生了错误。实际上,由局部刺激(local
stimulation)产生的颜色有赖于一般的空间组织知(spatial
organization),包括大小、形状和方向,这些东西都是由它产生的。如果人们将不同的术语互换位置的话,这一命题仍然是正确的。在先前的讨论中,这种相互联结(interconnectedness)已在某种程度上被详细地论证了。
三维组织
但是,还有一个方面(它的重要性表现在一切恒常性问题之中)尚未得到充分的研究。·我指的就是三维组织(tri-dimensionalorganization)。现在试图对它进行系统的表述是不可能的。它不仅需要整整一章的篇幅,而且,最主要的原因是,进行这种讨论所需的事实尚未获得。道理很简单,在该领域已经从事的大量研究(所谓的一些假设工作)被证明不再站得住脚,况且,相对而言,从组织观点出发所开展的研究极少,尽管这种研究即将来临。因此,在本章中我将仅仅提出若干论点,尤其是网膜像差(retinal
disparity)因素和所谓的深度标准结合问题(the problem ofthe combination of the dapth
criteria)。
网膜像差
三维组织本身并不是由我们充分强调的网膜像差引起的。网膜像差在产生三维组织中起着十分重要的作用,这一点已毋须叙述。这里,我们试图做的事情是把网膜像差视作一种组织因素,它有赖于组织。对此因素的传统处理方式是描述事实,而不试图对它们究根问底。一些相应的点被界定为这样一些点,当它们同时受刺激时,便产生一个物体的知觉,或者被界定为这样一些点,当它们受到刺激时,便会产生同一方向的知觉。于是,需要补充这样的说法,如果同一个地理点(geographical
point)被投射在两个不相一致的视网膜点上,它将出现双重性,除非这种像差的量十分微小:在这种情况下,该点将作为一个点被看到,但其位置处在凝视点前或凝视点后的平面上,也就是处在“核心平面”(nuclear
plane)上,这是根据像差的方向而言的。我可以省略细节,因为这些细节在大多数教科书中均能查到。为什么具有这些效应的像差未被提及,往往是因为人们假设了这样一个终极事实,即长波光的刺激引起红色的感觉,或者用这样一种术语来陈述——“有机体利用了一种距离线索”——实际上,学生的情况不会比第一种例子中情况更好些。
建立动态的像差理论的尝试
很清楚,我们目前正在试图建立的一种心理学是无法用这样一种陈述来满足的。对这种心理学来说,视觉世界是心物场内(in the psychophysical
fieid)组织的产物,而且,它还试图了解这种组织的过程以及决定这种组织的因素。网膜像差的各种事实,正如通常陈述的那样,是一些几何学事实。然而,我们需要的是动力学(dynamics)事实。我们想知道由像差的几何学产生的力量。最初的两个尝试意欲发现这些力量的性质,一个尝试是由勒温(Lewin)和佐久间(Sakuma)作出的,另一个尝试是由我本人(1930年)作出的。在下列讨论中,我将多少省略前两位作者所作的困难的然而有意义的重要贡献,仅仅提出我的著述中的若干论点。
网膜对应和网膜像差的界定
这是界说对应和不对应的第一个论点。首先,这样一种界定看来颇为简单:人们只须在外部空间选择某个点,看一看这个点投射在两个视网膜的哪些点上。如果这个点作为一个点被看到,而且在核心平面上被看到,那么,它投射于其上的两个视网膜点便是对应(corresponding)的两个点;如果用来投射的外部空间的那个点看上去呈现双重性,或者不在核心平面上,那么视网膜点便出现像差。如果人们用此方式探索两个视网膜,那么,他们就会发现,它的两个中心是一致的,所有的点在来自两个中心的同一方向上具有同样的距离。由此,人们已经达到有关对应点和不对应点的纯几何的或解剖学的界定,也就是说,一种纯几何学的方法,通过这种方法,一个视网膜上的任何一点,在另一个视网膜上具有相应的点。然而,若要把两个点的协调意义表述为对应或不对应,看来要比迄今为止出现的情况困难得多。假定我在左侧视网膜上选择一个点X1(1代表左边),并用上述方法在右侧视网膜上找到与X1相对应的点Xr(r代表右边);如果我不用“对应”这个词,我如何才能表述这一过程的结果呢?我可以说,Xr距离右侧视网膜中央凹与X1距离左侧视网膜中央凹不论在方向上还是在远近上都相同,Xr具有这样的特性,当它像X1一样受到同样的外部点的刺激时,眼睛的主人就会在核心平面上看到一个点。该命题的麻烦在于,它把外部空间的一个点作为它的条件之一,也就是说,它对接近刺激(Proximal
stim-ulus)来说是外部的某种东西,因而能对视觉过程不产生直接影响。双眼“无法知道”它们是否受到同一个外部点的刺激;某些类型的接近刺激将会产生一个点时的知觉,尽管实际上存在着两个点(例如,在立体视镜中),这种知觉与实际上只有一个点时而看到一个点时的效果是十分一致的。因此,我们必须试着从我们的对应界定中把距离刺激去掉,而且,完全按照接近刺激对它进行表述。人们可以试着做到这一点,他可以说:当两个对应点以同样方式受到刺激时,那么,结果就会在核心平面上看到一个点。由此可见,刺激的相等对于对应的界定来说是必要的,也就是说,它是超越纯几何学的某种东西了。
对于对应点来说是正确的东西,对于不对应点来说也同样是正确的。如果我们说,Yr是对X1的不对应,那么,这就意味着,当Yr和X1这两个点受到相同刺激时,结果不会在核心平面上看见一个点——而是看到两个点,或者其中一个点不在核心平面上。
像差的动力学

上述这种对应和不对应的界定,尽管并非完全恰当,但却涵盖了大量的事例。只要正确理解“等同性”(equality)一词的含义,我们便可了解其内涵所在。等同性并非指辐射的相等。如果在立体视镜的左半部插入一个灰色面,面上有一蓝点,并在立体视镜的右半部插入一个相等的面,面上有一红点,这些点在它们各自的面上差不多具有相同的位置,然后让一个具有不一致颜色的点在红蓝两色之间变化,该点将会被看到。这一情形证明,如果我们用辐射的等同性去界定刺激的等同性,那么,若干一致的点尽管受到不同的刺激,仍会产生正常的结果:在核心平面上有一个可见的点。在第二个实验中,立体视镜的两侧都是白色的,每一侧在一根想象的水平线上都有两个黑点,该想象的水平线将这些场一分为二,但是这些点在两侧彼此之间距离不同(参见图80)。在这种情况下,只有两个点,例如被凝视点F1和Fr,能够落在一致的点上,而P1和P’r则必须被投射在不一致的点上。如果这种不对应不是太大的话,那么,观察者将总共看到两个点,每一个点与一对刺激点相对应,P点将位于右方,并在F点之后,因为P1和P’r都是不对应的点。这种情况与我们的不对应界定相符,因为P1和P’r这两个点在颜色上是相等的,而Pr点与P1点在右侧相一致,它位于P’r的左边,所提供的刺激不同于P1提供的刺激,与此相似的是,P’1与P’r在左侧相一致,它反射了不同种类的光。但是,我们从第一个实验中看到,在有些条件下,一致的点尽管受到不同的刺激,却仍然产生正常的效果。那么,为什么它们在这里却不一样了呢?当我们重新阐述这个问题时,这个问题的意义可能会变得更加清楚。我们把两种不同的刺激模式投射于两个视网膜上。对于一个视网膜上的每个点来说,在另一个视网膜上有着对应的一个点;结果,可以完全正确地说:不论这些刺激模式是什么,它们总是对一致的一些点的全体进行刺激。这种说法,尽管从几何学上来讲是完全正确的,但却是不恰当的。它没有给不对应的点留下任何余地,这些不对应的点必须被引入,以便解释除了最简单的刺激种类以外的结果。换言之,由两个视网膜模式构成的刺激效果,除了在特定选择的例子中以外,不会与我们第一次实验中的效果相一致。在第一次实验中,两种不同色彩的点投射在两个视网膜的一致点上,结果,处于变化的和中间的颜色的一个点在核心平面上被看见。作为一种替代,这种刺激通常导致一种深度轮廓(depth
relief),表明不对应点决定了效果。这就意味着:在两个网膜上的进行合作以决定知觉组织的成对的点或线将有赖于两种网膜模式。这并非几何学或解剖学事实,而是动力学事实。在每一情形里,一定存在着实际的力量,它们导致一种协调而不是另一种协调。这些力量的直接根源并不在于网膜模式本身,因为它们是分开的,从而难以相互作用。相互作用只能在下列场合发生,即相互作用过程始于两条视神经束(optical
tracts)通过网膜模式在大脑里的会聚。这些过程将按照它们的结构特性而相互作用;也就是说,图形与图形相互作用,背景与背景相互作用,而不是相反;一条曲线中的一个独特的点与另一条曲线中的相应的独特点相互作用,不论它们是否被投射于一致的视网膜点上,等等。换言之,正是这些对应点和不对应点的概念成了组织概念的前提。
根据这个观点,我们可以回顾一下我们的两个立体视镜实验。在第一个实验中,各自位于体视镜一边的一个蓝色点和一个红色点将相互作用,每个点成为场内的唯一图形。正如我们将在下一章里看到的那样,眼睛能以这样一种方式进行自我调节,也即这两个点都被投射在一致的视网膜点上,这个事实是由同样的原理来解释的。可是,在我们的第二个实验中,同样的论点只应用于一个对子点,即F1和Fr,如果F1和Fr落在一致的视网膜点上,那么,其他的两个点便无法落在一致的视网膜点上。然而,它们将相互作用;由于两个图形彼此贴近,因此它们将彼此吸引,它们的联合为其他两点的联合所阻止。但是,没有理由可以说明为什么P1应该与属于背景的pr相互作用,或者为什么P'r应该与P'1相互作用。上面提出的问题(见边码p.269)得到答复,而且,这种答复已经为我们提供了对于双目视觉动力学的一种顿悟。在“结合区”(“
combination
zone”),也即我所谓的心物场的那个部分(在该心物场内,一些过程始于双目结合),当我们用两对点子进行第二种实验时,产生了一种应力(stress),这是一个最简单的例子。我们现在引入一种假设,如果不对应不是太大,那么,这种应力便会导致两个互相吸引点子的统一,与此同时,也导致了深度轮廓,即一个单一的点比另一个单一的点出现得近些或远些。这个假设是与我们关于知觉组织的整个陈述相一致的,因为它把一种明确的结果归因于明确的力量。这样的假设也是不完整的,原因在于它无法推论为什么这种应力(根据这种应力的性质,它应当导致统一)产生了深度轮廓。事实上,人们可以争辩说,以P1和P'r点的统一不可能像F1点和Fr点之间的统一一样,因为后者把场内的应力减至最低限度,而前者却创造出应力,用纯空间术语来说,两种统一之间唯一可能的差异是深度差异。即便这样,下面一些情况仍然得不到解释,即为什么类型或方向的不对应会使统一的区域接近,而对立的类型的不对应却使统一的区域远离,还有一种情况也得不到解释,即为什么这种结果或多或少地限于与纵向的不一致正好相反的交叉的不一致上面,在我看来很有可能的是,对这些事实的解释必须在视觉部分的结构中才能找到,也就是说,在永久性的内部条件中找到(这是第三章已经解释过的)。
某种实验证据
我将引证三个实验以支持这一假设。前两个实验表明由图形因素引起的合作的网膜区域的选择,第三个实验支持了下列假设,即深度效应是由结合区内的应力产生的。第二个实验可以追溯至赫尔姆霍兹(Helmholtz)的研究(Ⅲ)。在一架立体视镜里呈现两种透视图,如果其中一幅透视图是在白纸上画上黑色,另一幅透视图是在黑纸上画上白色,则立体视镜的效果不会改变。为了分析这个实验,让我们考虑并未投射在一致的视网膜点上的两幅透视图的对应角。如果左角是黑色,那么在另一只眼睛里的对应点也受到黑色的刺激,白色角在另一只眼睛里对一个非一致点进行了刺激,它在左眼的一致点也依次受到白色的刺激。假如P1和Pr,G1和Gr是两对有关的一致点,那么我们便有下列的刺激:
表8
然而,在这些一致的和相等的刺激对子中,以P1和PR为一方,G1和Gr为另一方,尚未相互作用,而是P1与Gr,G1与Pr相互作用;原因在于两个相互作用点在场组织中产生了相等的结构部分。
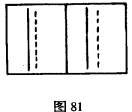
第二个实验是由我本人实施的(1930年)。它极其简单,如图81所示。两组成对的线呈现在一架立体视镜的不同侧面,其中实线上的一点得到凝视。两条虚线以这样一种方式绘出,即一侧的点于与另一侧的白色间隙相对应,而且,左侧的虚线比右侧的虚线更靠近实线。从几何学角度讲,左侧的一个点与右侧的白色相对应;此外,从原子论角度讲,右侧(像左侧受到一个点的刺激那样接受同样的刺激)没有不对应的点。让我们把左眼中接受一个P1点的刺激的这个点称作右眼中Pr的对应点,右眼中的这个点受到与左眼Gr点相对应的一个间隙的刺激,而它的一致点则是左眼中的G1。于是,刺激图式如下:
表9
首先考虑一下不同的视网膜点,为什么P1该与Gr合作,而不与Pr合作,这几乎是没有理由的,因为两个点都受到了同等的刺激。然而,如果我们想要阐述发生了什么,那么,这恰好是我们必须说的东西;观察者总共看到两条线,一条线与立体视镜幻灯片的两条连续线相对应,而另一条线则与两条虚线相对应,后者尽管不需要连续,但也像图80中的P点那样位于另一条线的后面。实际上,这一实验证明,相互作用并未发生在点与点之间,而是发生在整个线段与线段之间,也就是说,发生在单一的过程之间,这些过程始于由黑点分隔的每只眼睛。这些线条相互作用,因为它们是图形;不对应的一些点开始起作用,因为每个点是一个较大整体的一部分。在这两个实验中,业已证明,组织的因素抉择了哪些视网膜区域会导致相互作用的过程,哪些视网膜区域则不会导致相互作用的过程;与此同时,对应区域和不对应区域之间的差异被认为是受到解剖学的制约的;组织因素决定解剖学上的对应部分或不对应部分是否相互作用。勒温和佐久间试图更进一步,并且表明,对应和不对应本身是可以由组织因素决定的(p.334)。然而,我不能确信他们两人提出的证据是否严密,我省略了对他们独创性实验的描述,而满足于提及另一种更极端的可能性。
第三个实验是由杨施(Jaensch)于1911年实施的,该实验的目的是为了表明不对应本身并不产生深度。如果将三根垂线作这样的安排,其中两根垂线位于一正面平行面上,第三根垂线在两线之间并处于该正面平行面之前,于是,观察者会看到一种楔状结构,该结构的边缘正指向着他,这是与视网膜意像的不对应性相符合的。但是,正如在杨施的实验中那样,当这些线是处于一个完全黑暗的房间里的发光的金属丝时,这种楔状结构的深度便大大减少,而且,如果中心线并不明显的话,该楔状结构甚至会一并消失,从而使三根线都在一个平面上被看到了。这一事实支持了我们的理论,即深度效应是由于场的应力,它以下列方式引起:如果前面的线投射于对应点上,那么,另外两根线便投射于不对应点上,从而在结合区的边界上引起了两对“线过程”(line
process),它们并不相符;在这四个过程中,两个过程是左边的,两个过程是右边的,它们十分接近,互相之间强烈地吸引,每一结果均导致单一过程。它重复了我们上面使用过的论点,也即我们在解释具有两对点子的立体视镜实验中使用过的论点。那么,为什么在黑暗的房间里楔状结构又变得扁平了呢?我们认为不对应的深度效应是由于结合区内的应力。结果,当没有深度效应出现时,我们必须假设这种应力尚未创造出来。其原因是不难发现的。在先于结合区的区域内,两根不对应线与对应线距离不同,而应力便产生自这样的事实,即通过它们在结合区内的融合,这种差异被消除了。在明亮的房间里,两根不对应投射线中的每一根线与大量的物体处于明确的空间关系之中,而在暗室里,唯一的其他物体就是那根对应投射的线。在明亮的房间里,两对不对应过程的融合比在暗室中须与更强的力作斗争;换言之,在“前结合区”(pre-combination
area),线条的位置在房间被照亮时比之处于暗室中时更强烈地被确定下来。因此,在前者的情形中,由融合产生的应力肯定会比后者情形中的应力更大。即便不对应的线条在没有深度效应的情况下也发生了融合,那必定有某种应力存在。由于在线条的方向中,这一点并不明显,因此它肯定存在于环境场(the
surrounding field)中,我们可以通过探索环境场来检验这一假设。
不同“深度标准”的结合
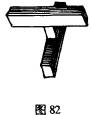
在第四章结束时,我们已经讨论了有关不同深度标准的传统观点。现在,让我们从另一观点出发回到这个问题上来。假如深度是空间组织的一个方面,而不同的深度标准是决定空间组织的一些因素,那么,我们该如何想象两者(深度标准/空间组织)的合作呢?在讨论形状和大小恒常性(constancy)时,我们发现深度产生各种因素以影响外观形状和大小(见边码p.235),我们还发现了一些难以符合下述观点的事实,该观点认为,不同因素是按照代数的加法原理而结合的。乍一看,这样一种原理似乎是我们的动力学理论所需要的。如果不同的因素充当了组织之力,那么,它们的结果也应当能用代数来确定。然而,存在着不同的可能性,对于其中一种可能性,我们可借弹簧秤的例子来说明。如果我们把5磅重的物体放在这样一个弹簧秤上,那么,秤的量尺将下降到某个点上,当我们再增加一磅重量时,量尺还会进一步降低;与此相似的是,如果我们不增加重量,而是向载有5磅重物的量尺在向上的方向上施加相当于一磅的力量,那么,量尺便将上升到一个位置,这个位置反映了倘若没有这种反作用的发生而重物恰恰等于4磅重的时候的那个位置。由此可见,量尺遵循了代数的加法定律。但是,现在我们把弹簧秤的量尺尽量向下拉,将钩子钩在一根水平杆的下面,使量尺固定在一个位置上不动。然后,如果我们在秤上再置上重物,量尺就不会移动,如果我们再施以上举的力,秤仍然保持不动,只要这股力并不足够强大,以致于冲破了水平杆的阻力的话。由此类推,我们了解到,不同的因素能以这样的方式进行合作,即当其中一个因素具有稳定性的最大效应时,其他因素则完全不起作用了。我并不认为这种类推是一种解释,而认为它是研究不同深度因素的一个指导性原理。为了说明这个原理是有效的,我将从施里弗(Schriever)的一个有意义的实验中作出推论。施里弗对若干孤立的和结合的深度标准进行了仔细的研究。把一个扭曲的H形周体(见图82)悬挂在一个黑暗的背景前面,然后,从两个不同点对它进行摄影。这两张照片便用来当作立体视镜的幻灯片。于是,交迭的不对应和阴影结合起来,成为深度因素。如果在这实验中,立体视镜的两张幻灯片相互交换,以便使原来属于右眼的物体现在被左眼看到,原来属于左眼的物体现在被右眼看到,那么深度的轮廓不会改变;有些被试指出,现在的空间并不那么令人印象深刻了,尽管仍然具有充分的可塑性,但却与一幅普通的透视图的深度不同。在这种情形里,网膜像差不会产生任何结果。如果网膜像差仍起作用,那么,整个深度轮廓将会颠倒过来,H形(图82)物体的梁看上去将像凹形的角铁(L形角铁)。对于这种变化的解释,也可根据弹簧种进行类推。上部的水平正面钢条可被视作一个物体,同样,下部那根水平方向的钢条也可被视作一个物体,不过,它被前者遗去了一部分。为了向前移动,必须直接穿越上面的钢条。然而,上面的钢条,作为固体物,是不能被穿透的,从而牢牢地把下面的钢条固定在它的位置上。确实,后者是一个实际的、地理的事物,而前者却是一个行为事物(behavioural
thing)。但是,我们已经看到,所谓“事物”是许多行为物体的一种特性,我们认为,行为的“物体属性”在许多方面是与地理的物体属性或物理的物体属性相似的。对于这个假设,我们将在本章末尾详细地进行讨论,因为它解释了知觉的若干事实。
空间的方向错误
在作出上述这些评论以后,我们将结束空间组织动力学的讨论。然而,必须特别提及的是,现象空间或行为空间(pheno-menal or behavioural
space)具有一种特性,尽管我们在各个地方已经遇到过它。行为空间并非欧几里得(Euclidean)空间,而是方向错误(anisotropic)的空间,它在不同的方向具有不同的特性。必须区分方向错误的两个方向。一方面,图形和物体的组织创造了应力,这些应力并不限于分离的单位,而是在或大或小程度上对环境场发生影响。大家熟知的一些观错觉,诸如贾斯特罗(Jastrow)和松奈(Zollner)错觉,证明了这种效应,正如我在其他地方已经指出过的那样(1931年,p.1182,1931年a,p.1263)。另一方面,空间作为一种格局(framework),其本身是方向错误的,并通过方向错误决定了格局内部图形和物体的组织。我们已经强调了这样一个事实,即存在着主要方向,这些主要方向对组织产生功能性影响。
两种维度的方向错误
但是,即便在其主要方向上,空间也并非均等的(isotropic
)。所谓对垂直方向的过高估计也表明了水平方向和垂直方向的不等性;这种现象表现在除了圆以外的每一种图形的感知之中(参见考夫卡,1931年a,p.1228)。关于这种方向错误的其他表现,我已经在另一篇文章中(1931年a)提到过了,这里我将仅仅提及一下所谓的r运动。如果把一个图形作短时间呈现,那么它就以扩展的运动而出现,并以收缩的运动而消失「肯克尔(Kenkel)];两种运动都是从图形组织的动力学中产生的,这已为林德曼(Lindermann)、哈罗尔(Harrower,1929年)和纽曼(New-man)所证实。然而,这种运动的方向表明了空间的方向错误。林德曼和纽曼发现,一个正方形在水平轴上的运动要比它在垂直轴上的运动更为有力。林德曼还发现,这一情况对于圆和椭圆来说也同样正确。水平和垂直方向的另外一种方向错误是由J.F.布朗(Brown)于1931年发现的。在两种相等的运动中,一种在垂直方向上运动,另一种在水平方向上运动,前者似乎具有更大的速度。这一结果表明,该方向如同对垂直方向进行过高估计一样,但在数量上却大得多,对过高估计来说约达4-5%,而对速度差异来说约达30%。最后,奥本海姆(Oppen-heimer)也已发现,垂直方向构成了主要的运动物体的参照系(见下述)。
三维方向错误
然而,当我们考虑相对来说不是很小的表面,而是最大可能程度上的整个空间时,视觉空间的方向错误就变得格外清楚了。首先,它表现出第三维度在功能上与前两个维度有所不同。有关的实验资料不是太多,而且广泛地散见于各种研究之中。这些资料「诸如奥-福视角现象(Aubert-Foerster
phenomenon)」的心理学意义是由杨施发现的(1909年)。奥-福视角现象与那些决定表面大小的因素有关,其他的资料可在视觉运动领域收集到,还有一些资料则取自脑损病人的实验。
我选择了一些实验结果,它们充分表明了方向错误的一些事实。
1.表面色的丧失
我想起了盖尔布(Gelb)的两位病人,他们失去了表面色(surface
colours),这在第四章已经讨论过了。我们发现,对于这两位病人来说,与背景相分离的一个表面色沿所有的方向传播,但是,这种传播在第三维度中要比在第一、二维度中大得多。我们在第四章(见边码p.118)提供的解释可以用来表述方向错误。例如,病人望着白色背景上的黑色方块。视网膜分布是知觉组织的第一原因;场内的梯度(gradient)不仅创造了图形与背景的分离,而且还导致了它在一个平面上的定位。现在,对这些病人来说,这种定位是不完善的;白色背景有某种程度的“厚度”,而黑色图形是一个大得多的图形,并稍稍延伸到它的客观界线以外的地方去。这样一来,视网膜条件在前两个维度中产生的凝聚力(force
of cohesion)要比在第三维度中产生的凝聚力更为有效;由此可见,三个维度不可能完全相等。
2.第三维度的运动
另一种实验(在第二章已有描述)也表明了类似的方向,那就是虹膜光圈(iris
diaphragm)实验。借助虹膜光圈,人们可以在一间完全黑暗的房间里看到一个明亮的表面。如果光圈开着,白色圆圈便似乎趋近,当光圈闭合后,白色圆圈便退向远处——这种结果比起没有趋近和退远的可察觉的扩展和收缩来更经常发生。在这情况下,视网膜意像在前两个维度中的变化引起了第三维度的行为变化,它表明这些变化更容易产生,从而证实第三维度不等于前两个维度。
冯·席勒(Von
Schiller)通过视觉运动实验证明了上述解释,我们将在后面讨论这个问题。这里,引述一下作者的话已经足够了:第三维度中的断续运动(stroboscopic
motion)似乎比另外两个维度中的运动更为明显。
3.邻近性和清晰性
第三维度本身表明了方向错误,这是由于组织与呈现的物体距离具有差别。我们已经知道当物体被看成较近而不是较远时,同样的视网膜意像会引起较小的行为物体的大小(这一事实构成了大小恒常性的基础)。与此同时,当物体受到高度照明时,它可以更清楚地被见到,而且通常显示出“更明亮”。一方面是外表大小,另一方面是清晰度和明亮度,两者之间的联系在“视物显小症”(micropsia)中尤其明显。这种视物显小症很容易产生,只须将低折射力的凹透镜放在眼睛前面,便可引起视网膜意像的减小,这种情况与实际知觉物体所观察到的缩小是不成比例的。杨施把这一结果称为科斯特现象(Koster
phenomenon)。赛恩默斯(Sinemus)最近表明,视物显小症既改变白色(或者,更一般地说,改变物体颜色)又改变明度。这些变化取决于客观照明的强度。就我所能看到的而言,这些作者尚未提及上述事实与表面距离的关系。然而,有一种简单的观察,它对大多数去剧场看戏的人来说是相当熟悉的,我认为这种观察无疑建立了这种关系。把一架普通的望远镜在长度上放大2.5-3倍,但是,当我们用这架望远镜观看舞台上的演员时,演员的身高看来并不比用肉眼看到时更高些。人们可以使自己确信以下的事实,如果一个人用下列方式使用望远镜,即把左侧目镜放在右眼的前面,让左眼保持裸眼状态,接着转动望远镜,使同一个外部物体的两个图像(一个正常图像,另一个放大图像)并排地出现。于是,观察者便会知觉到它们之间在大小尺寸方面的巨大差异;然而,当这个人恢复到正常地使用望远镜时,物体便显得比放大的图像小得多。与此同时,通过望远镜看到的物体显得更清楚和更接近。由此,视网膜意像的放大对于行为物体具有三种不同的效应:(a)它使行为物体稍稍放大,这是最不显著的效应;(b)它使行为物体变得更加清楚;(c)它使行为物体变得更加趋近。效应(a)证明,尽管听起来有点似是而非,但使用一架剧场望远镜确实产生了“视物显小症”——但是,只要我们不把用望远镜或不用望远镜看到的物体大小进行比较,而是把看到的物体大小与各自的视网膜意像进行比较,这种似是而非便会消失。在这一例子中,也有可能在其他一切例子中,较大的邻近性伴随着较大的清晰性。
我认为,奥-福视角现象(Aubert-Foerster
Phenomenon)表明了同样的空间方向错误。可是,由于弗里曼(Freeman)表明,引起它的条件并非像杨施原先认为的那么简单,因此,我将省略详细的讨论,并且仅仅提及这样的论点,即奥-福视角现象表明了视力敏锐性对所见距离的依赖,在这个意义上说,用视角来测量的敏锐性,在小距离时要比在大距离时更大。
4.天顶-水平线错觉
另外一种方向错误已由天顶-水平错觉所证明(见第三章)。我们能以这种方式进行系统阐述:我们在一名观察者的居中平面上描绘若干具有不同半径的圆,把他两眼之间的中点作为圆心,并使它们在一个水平半径和一个垂直半径的末端附着相等的圆盘(水平半径用
h1,h2,h3…表示,垂直半径用v1,v2,v3…表示,换言之,我们使用具有不断增加的半径的圆周),而且,我们首先比较相同圆上h和V的外观,然后把一个hk和Vk之间的关系与一个hn和Vn之间的关系进行比较。于是,我们发现,在趋近的圆上,行为的hn和Vn将相等,但是,随着不断增加的距离,h看上去会比相应的V增加更大。这种现象说明,按照空间的方向错误来表述的大小恒常性,在水平维度上要比在垂直维度上更大。正如我们在第三章的讨论中所看到的那样,依附在h和V之间居中位置上的一些圆盘将会表现出一种中间大小(intermediate
size),它表明方向错误遍及整个空间。这种方向错误不仅与表面大小有关,而且还与表面距离有关——天空的形状不是球状的,而是水平的;但是,距离的方向错误的量化方面还没有像大小方面那样被很好确定。
方向错误和位移:冯·阿勒施的实验
我们把这种方向错误与下面的事实联系起来,即我们都生活在地面上,而且主要以水平方向在地面上穿行。如果这种联系是有效的,也即它并非从经验主义角度进行解释,而是作为整个神经系统结构的一种结果,那么,具有不同位移(locomotion)的动物空间也应当是不同的。这一论点是由冯·阿勒施(VonAllesch)提出来的,他进行了一项实验测试,用人类被试的若干空间功能与一个动物的空间功能进行比较,该动物生活于树林中,其位移主要是攀爬和跳跃。如果空间不对称且与位移方向有联系的话,那么,人们可以指望,对于这样一种动物来说,垂直方向将优越于水平方向,月亮位于天顶时将比位于地平线上时要显得大一些。冯·阿勒施选择了狐猴作为他的被试。他并不测试能够直接证明上述结论的一种功能,而是测试了两种其他的功能,那就是,距离分辨和大小分辨,他发现,对人类来说,当用笔直向前的物体进行测试时比用笔直向上的物体进行测试时,前者的阈限更加细微。对于他所测试的动物来说,也是一样。也许,单凭这样一个实验尚不足以证明这样的假设。不过,该实验看来是十分有意义的,使之具有相当程度的可能性。人们期望,新的实验将决定这一特别重要的问题。
5.方向错误和恒常性
知觉空间的方向错误与大小和形状恒常性有密切关系,从而与物体的恒常性也有密切的关系。与大小恒常性的关系是已经提及过的话题。现在,我补充几句关于形状的问题。我们来回顾一下关于旋转图形(椭圆,矩形)的讨论,我们可以这样说:一根网膜线越是出现在对凝视线来说正常的一个平面之中,它看上去就越短,也就是说,它的整个长度越是显得与观察者保持等距。我们把对这一结果负有责任的那些应力解释为构成心物空间的方向错误。由于这种方向错误导致对现实的确切认知,从而比均等的空间(isotropic
space)导致更加协调的行为,人们可以把它与它的生物利益联系起来。然而,在我看来,只要人们对这两个术语之间的因果联系尚未形成概念的话,这些推测便是具有欺骗性的。利益本身并非原因。一种发生学解释(geneticexplanation)(它认为个体经验只起很小的作用)将不得不考虑这一事实,即知觉空间的方向错误通过或多或少消除实际空间中的透视效应来实现其认知结果。
可见运动
迄今为止,行为世界被陈述为是由不变的刺激引起的,从而相应地包含了一些静止的物体。这样一种含蓄的假设把我们的研究领域限于一些在十分特殊的条件下才能实现的独特事例上。通常,运动的物体位于我们的场内;例如,此时此刻,在我自己的场内便有我的钢笔,我的手指使它在一页纸上移动;现在,有一只嗡嗡叫的苍蝇飞过我的视野,而且,一俟有客人进入办公室,他不会如此刻板地冷静,以致于产生不变的视网膜意像;但是,即便我独处一室,我也会靠在椅背上,开始思考一个问题的解答方法,我的双眼不会固定不动,而是改变它们的视线,从一个物体移向另一个物体,从而产生视网膜图像的改变。在第一个例子中,实际的运动物体出现在场内,视网膜图像的转移导致了物体的行为运动,不论我盯着一个非运动的物体看还是追随一个运动的物体,该转移都导致了物体的行为运动;在第二个例子中,当我的双眼在静物之间漫游时,这样一种视网膜转移便不具有这种结果。尽管两个事实密切相关,但是,对于第二个例子,我们将在第九章进行充分的讨论,也就是说,在我们介绍了自我(Ego)以后,再来开展讨论。这里,我们把注意力主要集中在第一个例子上面,即便我们尚不能完全避免涉及第二个例子。因此,让我们现在转向可见运动(Perceived
motion)的理论上来。下述的事实是大家所熟悉的,即视觉运动的论述是格式塔心理学问世的标志。威特海默(Wertheimer)于1912年根据他的经典研究简要地阐述了若干新的原理,借以构成格式塔心理学理论。即便我们在其他领域发展了这些原理,并在其他事实的帮助下发展了这些原理,我们仍试图用威特海默的著述来讨论我们当前的课题,这样做也遵循了该领域的心理学发展史。然而,我将选择一种不同的方式,根据现在可以得到的所有知识,系统地描述各种事实和理论,并在进行这样的尝试时,将注意力更加集中于嗣后问世的著述,而不是先前的著述。尽管人们对先前的著述相当熟悉,但是,它们充斥着一些实验,这些实验驳斥了当时为人们所推崇的理论,今天看来这些实验已经过时了。由于我已经陈述过这个课题(1919年,1931年),而且在1931年刊布的一篇论文中予以相当确切的表述(这篇论文包含了大量细节,这里将省略),因此,如果再这样做,便是单纯的重复了。
威特海默的论文以及随之而来的一些著述主要地或专门地讨论断续运动(stroboscopic
motion),也就是可见运动是由静物产生的。由于这一发现已经毫无异议地被证实了[威特海默,瑟麦克(Cermak)和考夫卡,邓克尔(Duncker),1929年;布朗,1931年,范·德·沃尔斯(Van
der Waals)和罗洛夫斯(Roelofs),
1931年」,因此,就心物动力学而言,在断续运动和“实际”运动之间没有任何差别可言,也就是说,可见运动由实际运动的物体所产生。为此,从后面的例子开始我们的讨论,看来较为合适,因为诸如此类的例子是十分常见的。
可见运动理论的一般原理
我们从非常一般的陈述开始,这是由苛勒(kohler)明确地加以阐述过的(1933年,p.356)。可见运动的生理相关物肯定是整个生理过程模式中的一种实际的变化过程。假定知觉场除了有一个点作穿越它的运动以外是完全同质的(homogeneous),那么,这个点的运动便不会导致我们所假设的这样一种变化,因为在整个同质场里面,它处处展现同样的应力,一切位置从动力上说都是彼此不可区分的。在这样的条件下,知觉不到运动,而且,尽管这种条件是不可实现的,但它的讨论仍然阐明了那些可以实现的条件的意义。在这个意义上说,我们的知觉场决非完全同质的。甚至在完全黑暗的情况下,我们的知觉场还有上和下、右和左以及远和近之分;如果穿过知觉场的一个点改变了它与视网膜中央凹的距离,则除了按照这三种决定而改变其位置以外,同时还通过了具有不同功能特性的区域。整个场的异质性(inhomogeneity)以及异质场内一个点的移置,是引起心物运动过程的两个必要条件。这是因为,在异质场内,一个物体的运动改变了它与整个生理过程模式有关的动力条件。据此,我们可以推论,比起较少异质的场来,较大异质的场更有利于引起可见的运动。这样的推论已为事实所证实。一切运动阈限在相对来说同质的场内要比在异质场内更高一些(见拙作,1931年,p.1194),而且,客观上用同样速度运动的物体的似动速度,在异质场内要比在相对来说的同质场内运动速度更大一些(布朗,1931年,P.218)。这两个事实紧密相关,这是布朗(1931年b)已经证明了的。
我们的结论是,视野中的可见运动以那些与场的其余部分相关的物体移置为前提,这一结论也符合我们据此开始讨论的那些事实。如果物体在地理环境中移动,那么,不论我们凝视它们还是一个物体处于静止状态,它们的视网膜意像会由于其他物体而被移置,可是,眼睛穿越静物的运动将使这些静物与周围物体的关系保持原封不动。确实,眼动也产生了视网膜上图像的转移,从而肯定具有某种可见运动的效果,不过,这种运动不该属于场物体。我们在后面将会看到,我们对我们眼睛的知觉,或者甚至对“我们自己”的知觉,像运动一样,是这种转移的结果(邓克尔)。
邓克尔的实验
这种关于运动知觉起源的观点必然导致十分明确的实验。邓克尔于1929年完成的杰出研究完全取决于上述观点。假设场处于同质的黑暗中,其中只包含两个发光物体,一个发光物体处于客观运动状态,另一个发光物体则处于静止状态。于是如果运动的速度不是太大的话,那么,主要的决定因素将是两个物体的相对移置。根据我们的理论,它导致可见运动,不过,我们的理论并不允许我们去推论这些物体中哪个物体是运动的载体,只要它们相对移置,没有任何其他因素起作用便可。但是,我们的理论包含了其他概念,它们提示了解决这个问题的一种方法。
参照系
让我们回到物体和格局的区分上来,回到格局比格局内的物体更加稳定的知识上来。如果我们将此用于运动的情形,我们必须推论出以下的命题:如果两个场物体中的一个具有对另一个场物体的格局功能,那么,这个场物体将被看成是静止的,而另一个场物体将被看成是运动的,不论这两个场物体中哪一个实际上是运动着的。另一方面,如果这两个物体都是事物,那么,在对称条件下(在它们之间凝视或者自由地漫游式注视),两者将以相反方向运动。
上述两种推论在邓克尔的实验中均得到证实。他还发现「特林(Thelin)在他之前已经发现」,对两个相等物体之一进行凝视,倾向于使它成为运动的载体,不论它在客观上运动与否,对此事实,他暂时用物体-格局的区分来解释,或者用图形-背景的区分来解释,凝视点保持了它的图形特性,而非凝视点则成为背景的一部分。邓克尔的发现为奥本海姆(oppenheimer)的一项研究所详细证明,该研究报告刚刚问世。对于奥本海姆的研究结果,我只想提出两点:(1)物体的相对强度起着一种作用,较强的物体倾向于成为较弱物体的参照系(frame
of
reference);因此,如果其余条件保持不变的话,较强的物体将处于静止状态,而较弱的物体则处于运动状态;(2)物体的形状的下列方式决定似动运动(apparent
motion):如果两个物体之间的相对移置以这样的方式发生,即它的方向刚好与一个物体的主要方向之一重合,而不与另一个物体的主要方向之一重合,那么,前者比后者将倾向于看上去移动得更远些。由此可见,相对移置并不决定运动载体,而是在这些条件之下,决定了运动的量。这是一个不变因素(invariant),不论一个点在运动时被看到,还是两个点在运动时都被看到。事实上,正是邓克尔引入不变因素这一概念(尽管他并没有使用这个术语),这种不变因素的概念在我们讨论的知觉组织方面硕果累累。如果只有两个物体参与其中,那么,不论是两个物体彼此相等还是其中一个是另一个的格局,运动振幅的不变性都能适用。一俟第三个物体进入,这种不变性便不再保持。如果a是b的格局,b是c的格局,而客观上b是运动着的,那么,就会发生两种不同的相对移置;b在它自己的格局a里面改变了它的位置,而C则在它的格局b里面改变了它的位置。由此条件产生的两种可见运动之和将比下述情况更大,即如果b的运动恰恰与先前一样,而物体a或物体c却被移去,由此产生的可见运动与上述的两种可见运动之和相比,前者将会更大。邓克尔讨论了第三种物体和其他两种物体之间的可能关系,并且用实验方法指出,对可见运动的影响有赖于它们之间附属(appurtenance)的种类和程度。格局的多元性,或者参照系,还具有另一种重要的效应,该效应首先由鲁宾(Rubin)于1927年予以确认。他那独创的精心设计的实验由邓克尔给予补充。这里,我将仅仅讨论一个十分简单的例子,正因为它为人们所熟悉,从而显示出其独特性。如果我们连续地观看地面上滚动的车轮,那么,我们可以同时看到两种运动,一种是圆周运动,一种是直线平移运动。实际上,轮子的每一点除了轮子中心以外,都在描绘旋轮线(cycloids),它的形状与圆的形状完全不同;而轮子中心则进行了纯粹的平移运动。但是,轮子的各点都以轮子中心作为它们的参照点,而中心本身则涉及到一般的空间格局,或者说,当房间处于黑暗状态时,轮子中心则涉及到观察者自己(参见下一段)。实际观察到的双重运动是这种参照系分离的结果。如果在轮子转动时,轮子中只有一点(不是轮子中心)可以看到,那么,旋轮线曲线上的运动便可见到。如果加上轮子中心(邓克尔),那么上述现象便立即发生变化,不同的现象产生了,它部分地依赖于轮子的运动速度,而轮子的全部运动具有这样的共同特征,即边缘的点描绘出旋转的运动。如果我们不去加上轮于中心,而是加上像第一点一样的同心圆上的一点,那么,根据鲁宾的实验(他是以稍稍不同的运动模式进行实验的)进行判断,我们便可看到两个这样的旋轮线运动。如果我们增加这些点的数目,便可以很快得到正常的轮子效应,也就是说,我们看到所有的点围绕一个看不见的中心旋转,与此同时还看到平移运动。
作为场物体的自我
读者可能提出的一种异议将把我们引向一个十分重要的概括。我们已经选择了一个最简单的例子,在该例子中,两个物体都在场内。但是,有可能也看到运动中的一个点。这难道不与我们的理论相冲突吗?如果我们的考虑仅限于“环境场”的话,那么将会发生冲突,不过,这样一种限制将是不适当的;我们在不同场合曾经看到,场过程不可能在不包括自我(Ego)的情况下进行详尽的处理。自我如何适合我们的理论将在后面两章加以讨论;在我们讨论的这一点上,就其本身而言,我们必须把它视作一个场物体。一个点的运动是两个物体的彼此移置,也就是说,这两个物体是点和自我。实际上,当场内有两点时,我们需要处理三个物体。然而,邓克尔成功地排除了自我的影响,他通过缓慢的速度和小的偏移来进行研究,结果使它们对自我来说成为阈下的了,或者是阈上的了。如果它们是阈下的话,那么,仅仅两点的相对移置便具效果;如果它们成为阈上的话,那么便会出现新的结果。作为第三物体的自我可以如此强烈地与两点中的一点结合起来,致使它参与到它的运动中去。这种结合是通过凝视来达到的。一个被凝视的物体并不改变它与自我的视觉体系的关系,不论它在客观上是运动的还是静止的。因此,在用点来进行的实验中,对客观上静止的点进行凝视的被试看到该点处于运动中,并同时体验他们自己眼睛的活动(邓克尔,P.201)。如果两个物体之一是一个将另一个点封闭起来的矩形,而且,如果这个非运动的点被注视着,那么,“一个人关于静止的自我印象便丧失;空间水平成为不稳定的了,甚至会发生晕头转向现象,即一个人觉得自己的身体僵硬地与那个点相联系,沿着那个(在现象上或多或少静止的)矩形移动”(邓克尔,p.206)。
因此,“自我”的表现如同任何其他场物体一样,这种观点可由两种普通的观察来证实:月亮看上去从浮云中穿过;当我们站在桥上,凝视着水中的一座桥墩时,我们似乎在溯流而上。这两种情形的道理是一样的,被闭合的物体载着运动,而第二个例子中的自我则参与了它的运动,因为通过凝视自我牢牢地与它结合起来了。
同一性:过程的融合
现在是陈述我们理论中迄今为止一直隐藏着的一个方面的时候了。我们把运动知觉解释成是由于过程模式的离位(dislo-cation)。如果一个物体被看作处于运动之中,我们便假设,与它的知觉相一致的过程分布(process
distribution)依照其他过程分布而被移置。这意味着,在可见运动的过程中,与一个物体相一致的过程分布在动力上保持同一,尽管它在其他过程分布的场内进行转移。由于我们迄今为止只在静止场内处理统一和分离,也就是说,不涉及时间,因此,改变其位置的一个过程的同一性(identity)便是一个新问题,正如我们将在后面看到的那样,它充满了有意义的结果。我们能以下列方式表述这个问题:如果一个光点穿过视网膜,那么,新的锥状细胞便会不断受到刺激,新的过程便不断地传入视网膜中心。锥状细胞是一些分离的结构,它们以具有可变强度的精细镶嵌遍布于视网膜上;因此,一个连续移动的光点会根据光点经过的雄状细胞数目引起分离的和有限的神经兴奋。在有些地方,这些连续的分离的兴奋肯定会变成一种连续过程,如果一个物体的移置发生的话;也就是说,始于锥状细胞中的兴奋不能彼此保持分离,而必须融合(fused)起来。由于在我们的例子中,它们在性质上和接近性上是相等的,因此这些神经过程将以巨大力量相互吸引,以致于它们的最终融合可从我们的前提中推论出来。
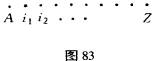
然而,我们可以设法改变这些条件,并且观察这些改变将对过程的融合产生哪些影响。可以改变的第一个因素是过程之间的距离。让图83中的A和Z分别代表两个终端的锥状细胞,它们被从左到右运动着的一个光点所刺激,而两者之间的一些点,如i1、i2……等等,均代表中间的锥状细胞。由此,网膜边缘发生的事件,即最终引起可见运动过程的事件,能以这种方式来予以描述。首先,在很短时间里(eA)A将受到刺激;然后,是一个很短的间歇(PA-i1),在这很短的间歇中,没有任何刺激发生;接着是刺激i1,嗣后又是另一个沉寂的间歇期,如此等等。按照我们的理论,在i1开始的兴奋与在A处开始的兴奋相融合。现在,让我们用一定量的时间eA先对A进行刺激,接着是一段沉寂的间歇期PA-2,这样一来,eA
和PA-2之和便等于光点以中等速度从A到Z通过所花的时间。那么,Z点上的兴奋会不会仍然与A点上开始的兴奋相融合呢?这一论点把我们从普通运动知觉引向断续运动知觉(perception
of stroboscopic
motion)。在最简单的一种断续实验中,我们先在A处呈示一个物体,然后,经过一段间歇期,又在Z处呈示另一物体,于是,相继地进行短时刺激的只有两个点,与两个邻近的锥状细胞相比,这两个点相隔更远。
断续运动和实际运动
历史上,这个可见运动理论首先是由断续运动发展而来的「哈特曼(Hartmann),苛勒,1923年a〕,在该领域中,由肖尔茨(Scholz)开展的一项专门调查证明了这一点。两种相继过程之间的融合产生自它们之间的吸引。这种力量的实际存在为下列事实所表明:两根断续展现的线条比起两根特久展现的线条,前者的出现彼此之间相隔较短距离,而且当它们在最适宜的运动中被见到时,其距离的缩短量达到最大值。
按照这一理论,断续运动问题在于建立一些条件,在这些条件之下,两个(或两个以上)分离的兴奋之间的融合便发生了,或者,当吸引对被吸引过程的影响足以使它们移置时(尽管这种吸引还不够有力以产生融合),便会产生这种现象,即两者或两者中任何一者被看到沿该路径的部分运动(威特海默的双重和单一的部分运动)。以这种方式进行阐述,断续运动问题与实际运动问题没有什么不同,正如我们已经看到的那样,在实际运动中,分别开始的过程也一定会发生融合。但是,由于在实际运动中,相互作用过程之间的空间距离十分之小,以致产生了很强的吸引力,结果使其他因素与它们相比就显得较小,并难以证明,而这些其他因素在断续运动中发挥更加重要的作用,在那里,由于过程之间的较大距离,力量显得较弱了。关于这些其他的因素,我提及一下时间的决定因素,也就是说,展现的时间和间歇;我还想提及一下强度(或者,更好的提法是,图形和背景之间的梯度),也就是说被展现物体之间的距离,它们的大小和形状。我们将在后面对它们进行讨论。
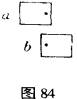
现在,让我们回到理论上来。断续运动和“实际”运动是基本相似的,这是对该理论有利的一个有力论点。要对一个静止物体通过与另一个物体的相对移置而“诱导”运动(induced
motion)进行解释,并不会引起任何新的困难。但是,还必须补充一点。邓克尔是通过将诱导物体相继地在两个不同位置予以展现,并将被诱导物体同时在两个相等位置上予以展现,来产生这种诱导运动的(p.224;参见图84,图中两次相继展现是以一个在另一个下方来表示的,而实际上它们是这样安排的,即两个点是重合的)。在特定条件下,断续移置中的闭合物体可能实际上表现为静止的,而被闭合物体(由于相继展现在同样地方)却包含了整个运动。在这种情况下,两个空间上相距甚远的刺激的融合并不导致运动,而两个空间上一致的刺激的融合却导致了运动。然而,这样做没有任何困难,因为按照我们最一般的原理,运动有赖于两个或两个以上场物体之间的相对移置,而对这些场物体如何构造不作任何限制。邓克尔所提及的实验说明了实际运动和断续运动基本相似。
似动速度:布朗实验
现在,让我们更为具体一些,不是去调查运动本身,而是去调查具体意义的运动。运动是有方向和速度的,两者反映在力学和经验中。如果我们考虑实际运动的知觉,那么,看来没有什么问题;人们期望,似动速度(apparent
velocity)在心理学的可能范围内等于实际速度,或者简单地依赖实际速度。这里,所谓心理学的可能范围是指阈下和阈上之间的范围。然而,J.F.布朗(J.F.Brown)的著名研究表明,这种观点是错误的。我们目前暂不考虑由这个问题(实际速度被我们选作我们的标准)产生的困难,物体本身的速度,即距离刺激,或者物体的视网膜意像的速度,即接近刺激,都呈现出:只有当距离刺激与观察者处于同样距离时,这两样东西才会紧密一致;这是因为,与同一种距离速度相一致的视网膜速度随距离而成反比地变化。但是,暂且撇开这个问题不谈,布朗已经表明,一个被看作运动的物体,它的似动速度有赖于场和物体本身,也就是说,有赖于物体的大小和方向,而且,如前所述,也有赖于运动的方向(1928年,1931年)。在他的实验中,两种速度必须相互匹配。在两个光圈的孔径(diaphragrn
aperture)后面,图形被看作处于运动状态,这种运动是由两个旋转的鼓引起的,在鼓的上面一卷卷有图形的白纸伸展着,以形成没有尽头的带子。在每一次实验时,标准带子的速度保持不变,然而,可变物体的速度则发生变化,直到观察者判断两种速度相等为止。看上去相等的两种客观速度的关系便成为对客观速度和主观速度之间的关系的一种测量。
为了给这一程序提供一种具体想法,我将详细地描述一个实验。标准物和可变物都位于同样的距离,除了带子和图形以外,场是同质的(黑暗的房间,从后面照明的旋转带子);标准物S的光圈孔径为15×5平方厘米;可变物B的光圈孔径为7.5×2.5平方厘米;标准物上面的图形是一些1.6厘米的圆,彼此之间的直径间距为4厘米,而可变物B上面的图形是一些0.8厘米的圆,彼此之间的直径间距为2厘米。总之,B的大小恰恰等于S大小的一半。在S中,速度用VS表示,是10厘米/秒,而在B中,平均速度用VB表示(7名被试),它看来与VS相等,是5.25厘米/秒,VS/VB=1.9,或者近似等于人这意味着:如果在一个同质场中,一个图形在所有线条维度方面是另一个图形的2倍,那么在这个图形中运动的物体看上去具有同样的速度,如果客观上它们的速度是(或近似于)较小图形中运动物体的2倍的话。据此,我们可以推论,如果客观速度相等,在较小图形中的物体的运动速度看上去为较大图形中物体运动速度的2倍。这种结果可用各种速度、各种大小关系以及一些控制因素来证实。所有这些实验的结果由布朗正确地归纳如下:“如果在一个同质场中,人们可在运动场的所有线条维度方面变换其位置,那么,他就必须用一种相似的量来转变刺激的速度。以便使速度的现象同一性(phenomenal
identity of
velocity)得以产生。随着一个场的线条维度从1转变到10,Vs/VB的商也倾向于从1到10发生改变”(1931年,p.126)。
从我们的理论中可以容易地看到,场必须同质,以便使这种结果成为现实。如果场是异质的,那么用图形纸覆盖的光圈,以及在两个场内的移置,便不再限于具有不同大小的孔径的格局了,而是涉及那些在S和B的图样中十分相似的异质。结果,这些东西之间的差别应当减少,布朗已经证明了那种情况(异质性增加了业已提到过的似动速度;见边码p.282)。
如果只有一些维度发生改变,而其余的维度则保持不变,那么,速度方面的相应变化比起所有的维度都发生变化来,前者的变化肯定较小。这一情况在光圈孔径的长度变化、光圈孔径的宽度变化以及物体大小在一系列不同结合中的变化中已经得到证明。我将提供两个例子:在图形保持不变的情况下,S中孔径在长度上为B中孔径的2倍,那么商Vs/VB便是1.38,如果图形也发生变换的话,则商为2。如果光圈相等,图形大小不等,那么,较大的图形必须比较小的图形移动得更快,方能表现出相等。这就意味着:在相等的刺激条件下,大物体(在现象上)比小物体移动得更慢。
如果场除了照明量以外恰巧相似的话,那么,较亮场内的物体必须客观上比较暗场内的物体移动得更快,方能显得速度相等。“现象明度的增加减少了现象速度”(1931年,P.223)。
最后,朝着运动方向的一些线条,从现象上看,比起那些与运动方向呈直角交叉的线条移动得更快些。
从布朗的结果导出一般原理的可推断性
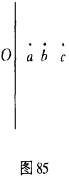
业已证明速度是一种受到场条件制约的现象。要想从布朗的结果中推断出一般原理,此刻尚无此可能。然而,有些暗示是可以适当考虑的。似动速度对维度的依赖可以从移置原理中推断出来(如果它能被具体阐述的话),以便使量化的预示成为可能。目前,我们尚不知道如何对移置实施量化。但是,一个简单的例子将解释我的原意(参见图85)。在两根终端线之间有一个点以一致的速度移动看,从左侧线的o点开始,时间为to,在时间t1时到达a点,如此等等,直到它一直到达右侧线为止。在第一个时间间歇t1-to期间,点和左侧线之间的距离从零向Oa转变,在下一个时间间歇t2-t1期间,距离的变化从Oa到Ob,如此等等,在相等的时间间歇期间,一切增长数都是相等的。但是,这些相等的距离增长数是否对引起可见运动同等有效?或者,先前存在的距离越小,增长数是否将更加有效?也许在下述形式中,即根据对数定律,相等的增长数并非同等有效,而是除以先前存在的距离后得出的相等增长商数。在那种情况下,点的移动离开O点越远,来自O点的进一步移置将变得更不有效,然而,与此同时,涉及右侧线的移置将变得越加有效,这两种变化以下述方式结合起来,即在路径的中央,同样的客观移置将对运动产生最小的影响。从量化角度讲,这一假设不可能正确,但是,同样不可能的是,绝对相等的增长数具有相等的效果。布朗本人报告说,在阈限实验中,运动先在光圈孔径的边缘出现,只是到了后来才在中央部分出现(1931年b)。从质化角度讲,如此的考虑导致这样一种推论,即较小的场一定比较大的场具有更大的速度,但是,只要我们的知识不超出目前所掌握的范围,那么,我们除了指出对布朗的转换定律(Brown’s
law of
transposition)负有责任的这样一种关系的可能性以外,便不可能做别的什么事了。在这些条件下,如果去猜测由运动着的物体的大小对似动速度产生的影响与光圈孔径的大小对似动速度产生的影响属同样类型,或者大小或容积是否会向运动着的物体提供一种惯性,这种惯性本身将会使较大物体运动得更慢,恐怕是不成熟的。朝着运动方向的线条比那些与运动方向成直角交叉的线条移动得更快,这一事实至少提示了这种严格的“动力”解释的可能性,这种“动力”解释从下列事实得到了支持,即在断续实验中,德西尔瓦(De
Silva)发现较宽的线条移动速度比较窄的线条移动速度明显地更加缓慢,后者的运动在大小和距离关系似乎不起作用的条件下更加平稳。
最后,明度效应成为可以理解的,如果我们把明度作为图形一背景的梯度来解释,作为图形的更强清晰度来解释,那么这是与布朗的仪器相一致的,也与他为场的强烈变暗效应所提供的描述相符合,在场的强烈变暗情形中,图形轮廓变模糊了(1931年,p.223)。我们可以下结论说,物体的图形特性越明显,它的运动性就越小。
提出这些建议(不仅为人们所需要,而且也能够得到实验证明)已经足够了。它们至少反映了布朗结果的理论可能性。
布朗的结果和柯特定律
我们现在从布朗和柯特(Korte)的研究中提取其他一些结果,也就是说,它们涉及到断续运动。从现象上讲,断续运动像任何一种现象运动一样具有一种速度,尽管没有与此相一致的物理速度,因为从物理角度看,不存在运动。但是,我们能够通过以下考虑来界说客观的断续速度。在断续的呈现中,一个点在tl时刻出现在A上,持续一定时间(e1),然后经过一段时间间歇P以后,另一个点在t2时刻出现在B上。于是,我们可以说,客观的断续速度是一个点所具有的速度,如果该点在t1和t2两个时刻之间实际上从A处向B处移动的话。假如用V表示客观的断续速度,我们可以解释v=AB/(t2-t1),或者由于t2-t1=e1
+P,v=AB/(e1+P)。最后,用s表AB,用t距离AB,用t表币e1+P,我们便得到v=s/t。
现在,让我们想象一下,我们已经成功地产生了一根线条穿过一定距离S的断续运动。于是,我们增加两根相继展现的线的强度。这样,根据布朗的结果,我们便可预言将会发生什么事情。由于现象运动在较亮的场内比较暗的场内速度更慢,因此,两条较亮的线将显得移动得更慢。为了使它们移动得像较暗的线一样快,我们必须增加其客观的断续速度v。只要我们增加s/t商数里的分子s,或者减少分母t,都可以达到增加客观的断续速度v的目的。这是因为,通过s/t,v得到了界说。实际上,如果s(距离)不小的话,那么,断续运动对距离、时间和强度的变化是十分敏感的;它不仅仅用速度的变化来对这些变化作出反应。如果t变得太大或太小,那么便看不见任何断续运动;在第一种情形里,两个物体是作为相继的两个物体而呈现的,在第二种情形里,则是作为同时出现的两个物体而呈现的。在相继出现和同时出现这两个阶段之间存在着一个最佳的运动阶段,在它的任何一边都有一些中间阶段围绕着(威特海默,1912年),我们省略了它们的细节,除了变得似动的速度差别以外。现在,我们可以把对改变强度的情况所作的推论阐述如下:如果我们增加以最佳的运动阶段得以产生的方式展现两根线条的强度,那么,现象将朝着相继阶段变化,它可以通过增加两个物体之间的距离,或者通过减少第一次展现和第二次展现之间经过的时间而被重新建立起来。由柯特在20年前表明的这一情况是正确的,柯特的前两条定律说的正是这种情况。
柯特的第三定律论述两个物体的距离和时间分配之间的关系。一俟我们把自己限于s和t之间的关系上面,我们便可以看到,如果我们再次从最佳的运动状况开始并增加s,那么通过界说,我们增加断续速度V=s/t。如果可见速度是断续速度的一种线性函数,那么,我们便应当以增加s的同样比例增加t,以便维持同样的似动速度;总之,如果断续速度和现象速度处于业已表明的那种简单关系的话,则s的一种变化要求t的成正比的变化。柯特的第三定律简单地表明,s或t的增加可被t中或s中的增加所补偿,毋须涉及量化关系。这条定律比其他定律更使心理学家感到迷惑不解,我必须承认,当我和柯特发现这一定律时,我自己也感到惊讶;在柯特工作时期,人们倾向于如下的想法:如果有人将两个相继展现的物体在空间上或时间上越发分离,那么,这个人就会使这两个相继展现物体的统一变得越发困难。由此可见,距离的增加应当由时间间隔的减少来作补偿,反之亦然。
与这一推断不相符合的事实驳斥了整个思想方法,正是由于该原因(如果不是由于其他原因的话),我仍然认为柯特定律是有价值的。直到我读了布朗的论文以后,我才见到了本文中提出的那种联系。在柯特定律中,令人惊讶的不是s和t直接地相互变化的事实,而是已经包含在柯特表格中的一个事实,该事实没有引起他(和我)的注意。然而,这一事实却由我本人和瑟马克在十分不同的条件下所进行的实验中明显地显示出来了,也就是说,s和t之间的函数不是成正比的函数,而是t比s增加得更慢。下列表格取自柯特,包含了最佳运动在三种不同距离上的t值,其中a=l/1000秒。
表10
|
距离(厘米) |
最佳运动的t值(σ) |
|
2 |
183 |
|
3 |
219 |
|
6 |
256 |
(摘自柯特,p.264)
人们看到,当距离为原来的3倍时,t值与原来的t值的比例为1.4:1。或者,如果我们在2厘米和6厘米的距离上计算断续速度的话,即v2和v6,那么,我们便发现它们的关系是v6/v2=(6/256)/(2/183)=2.l,而s6/s2=3。如果我们不是这样,而是选择3厘米和6厘米的值,我们便得到v6/v3=1.7,以及s6/s3=2;在这两种情形里,速度之比要比距离之比更小。将这些值与上面搞引的布朗的值(见边码p.289)相比较,实际速度的关系为vs/vB,其中S场的线性大小是B场的二倍(在长度和宽度上),然而图形是一致的。这里,与线性场大小Fs/FB=2的关系相一致的是vs/vB的商=1.38。正如在柯特实验中那样,断续速度的商比距离的商要小一些,因此,在布朗的实验中,实际速度之商比场的大小之商要小一些。
我们系统地阐述了布朗的结果。我们的观点认为,似动速度越小,场就越大。我们也可以把这样的阐述用于柯特的结果上去:一个在断续中移动的物体,其所通过的距离的增加会减少物体的现象速度。因此,当我们用增加s的办法来改变断续运动的群集时,我们产生了两种相反的结果。一方面,在纯粹运动的基础上,我们增加了断续速度v,另一方面,我们减少了v对可见速度的影响,因为较大的场具有较慢的似动速度。一般情况下,第二种影响不如第一种影响那般强烈,因此,为了对s的增加进行补偿,我们必须增加t,尽管增加的程度较低。只有在布朗的补偿定律站得住脚的那些例子里,这两种影响才会一起消除。
如果在两个场内,一切线性维度分别为f和nf,那么,相等的断续速度vns和vs一定在vns/vs=n的关系之中。因此,假如我们把t1和t2分别称为两个场内的时间,则(ns/t1)/(s/t2)=n,t1=t2。在这种情况下,而且只有在这种情况下,柯特的第三定律便无法坚持了。并非由于这种情况是个例外,而是因为它是一种限制情况,其中的两种影响刚好彼此抵消。这一推论为布朗所证实,他发现,当一个场的所有线性维度以同样比例发生变化时,断续速度也必须以同样比例发生变化,也就是说,尽管s改变,t必须保持不变。
当柯特定律被发现时(在布朗发表他的结果之前),该定律一直保持着纯经验主义的概括。一些作者在某些条件下证实了柯特定律,而其他作者,由于他们在其他条件下工作,从而未能证实这些定律。此外,瑟马克和我已经补充了一条新的定律,即区域定律(the
zone
law),它以某种形式限定柯特定律的有效性。这一定律认为,当t(和s)不断变小时,产生最佳运动的s-t结合的范围(区域)便不断变大,因此,在这范围内,柯特定律便不再站得住脚了。区域定律无疑是正确的,但是,我并不认为该定律一定能限定柯特定律的有效性。瑟马克和我的检验是最佳运动对分裂的检验,可是,我们并没有观察到似动速度。如果这些东西也予以考虑的话,那么,柯特定律大概也会在这些“区域”内站住脚。我还认为,同样的考虑也能对不同研究者的互相冲突的结果起调解作用。
即便作为纯经验主义的概括,柯特定律也有其自身的价值。柯特定律除了对断续运动理论(见边码p.293)所作贡献以外,它们还被我和瑟马克用来证明可见的断续运动和实际运动的动力相似性,这是用已在这里省略的一些论点和实验来加以证明的,从而使我们认识到运动和闪烁融合现象(flicker-fusion
phe-nomena)之间的联系,该现象是由布朗(1931年b)直接证明的,并由梅茨格(Metzger)在一种稍为不同的环境中加以证实(1926年)。在柯特定律和布朗定律之间建立起来的那种联系使它们上升到纯经验主义的概括,并且证明它们表述了知觉组织的基本事实。就其本身而言,它们并非真正的定律,而应当恰当地称之为“柯特规则”(Korte
rules),不过,它们是从一些尚未完全认识的基本定律中产生的。在柯特、塞马克以及布朗的结果之间的逻辑一致性(这些结果是在不同时间用不同的方式获得的)确实是一个有利于说明这些结果和推论之意义的有力论点。
运动和时间
布朗的理论推断及其实验的独创性把我们对运动过程的了解引向深入。我们已经讨论了现象速度和现象距离,还没有讨论现象时间。然而,如果不考虑时间因素的话,真正的速度界定是不可能作出的。在动觉(kinematics)中,速度被解释成ds/dt,对于不变的速度来说,它相当于s/t。那么,有否可能将这一界定转化成行为速度或经验速度呢?也就是说界定v=s/t,其中v代表现象速度,s代表距离,t代表时间。布朗不仅引入了这一假设,而且还用严密的实验对它进行证明(1931年a)。这一假设的含意确实是令人震惊的。假定我们有两个不同照明的等场(equal
fields)。我们知道,如果客观速度相等,那么,在较亮场内的似动速度vb比之较暗场内的速度vd要慢一些。明度差异,至少像布朗所使用的那种明度差异,并不影响似动的大小。因此,我们可以写出vd>vb,s/td>s/tb。由于在这一不等式中,两个分子是相等的,而分母不相等,则td一定小于tb,而且,由于客观上td=tb,则时间在较暗的场内一定会比在较亮的场内流失得快一些。这一结论不仅令人惊讶,而且不可避免。它使时间的经历成为一种新的受到场条件限定的特性,但其本身并不如此令人震惊;令人震惊的事实是,经历的时间应当受到与时间没有什么关系的场因素的影响。布朗对他的论点之逻辑并不满意,于是使用实验来检验其论点。在这些实验中,观察者必须把一个看到的运动的持续时间与由两种(视觉或听觉)信号所标示的时间间隔的长度作比较。后者的时间间隔保持不变,可是观察到的运动速度是变化的,直到它的时间长度与时间间隔看上去相等为止。如果两种运动群集的似动持续时间都等于标准持续时间,那么,它们的似动速度也必须相等。不过,我们从先前的实验中得知,为使这些速度看上去相等,较亮场内的实际速度必须比较暗场内的速度更大些。在一个特定的群集中,据发现vb/vd的关系为l.23。vb/Vd=(Sb
/tb)/Sd/td,并且由于Sb=sd,所以vb/vd=td/tb=1.23。
如果我们已知td或tb,我们便可预示另一个。为使看上去与由信号所标示的时间间隔具有相等的时间长度,较亮场内(tb)的运动持续时间必须是1.45秒(5名被试的平均数)。根据我们上一个等式,我们推断出td=1.23,tb=1.23×l.45秒=1.78秒。这充分证实了预见。
布朗以同样方式测试了有关各种其他群集的时间假设,包括场的维度的全部和部分转换,以及对或多或少同质场的假设。所得结果证实了预见,甚至当vS/vB的商(预见是以该商为基础的)由其他观察者所决定,而不是由那些对两种持续时间进行比较来证实预见的观察者所决定时,也是如此。实验足以证明一般的假设,这是毫无疑问的,我们可以认为这种一般的假设在下列情形中(即在尚未由特定实验所证实的情形中)也是正确的。如果我们把一切群集都包括在内(对它们来说,现象速度得到了研究),我们便可以说:时间在较小的、较暗的和较近的场内流动得较快,而且运动方向越垂直,它就越不处于水平状态;此外,速度的完全转换定律(the
law of complete transposition of veloci-ties)是与持续时间的完全转换(complete
transposition of durations)相平行的。
布朗的这些推断和实验开创了科研和推测的广阔领域。关于我们的时间经历的生理相关物问题,最近已由波林(Boring,1933年)进行过讨论,他充分意识到这个问题的困难,意识到以下事实,即这种生理相关必须是一个过程,或者说是一个过程的一个方面。苛勒关于运动(以及定位;见边码p.281)的论点在时间领域内同样得到了应用。在第十章,与此问题有关的某些假设将会得到发展。这里,我们仅仅指出,如果看到的时间与一个过程或一个过程的一个方面相一致的话,那么,发生在一个场内的一些过程的性质(不仅仅是场的其他特征)将决定场内发生的事件的持续时间。对于这个复杂问题尚未开展过研究,尽管布朗提及过这一事实,而且在其实验中予以证实,即“充满的”时间(“filled”time)在现象上比“不充满的”时间(“unfilled”time)更长一些。未来的研究可能会发现现象空间和时间之间的基本的相互依存性,这已为贝努西(Benussi,1913年,pp.285f.)和盖尔布(Gelb,1914年)在类似的实验中所指出,并为赫尔森(Helson)和金(king)的更为彻底的研究所表明,这里略去了后者的研究。
融合的选择
现在,我们转向可见运动的最后一个方面,让我们讨论上面(见边码p.287)阐述过的那个问题。我们对运动的解释(不论是实际运动还是断续运动)是把边缘分离过程的融合作为部分假设来对待的。我们现在调查一些因素,它们决定了与迄今为止所讨论的内容有所不同的融合。如果在断续运动中只有两个物体被展现,那么,即使发生融合,也只能在与这两个物体相一致的组织过程之间发生。但是,如果在这两次相继展现中,每一次展现包括一个以上的物体,那么,问题便发生了,也就是说,第一次展现的哪个物体将与第二次展现的哪个物体发生融合,换言之,哪种运动将被看到。同样的原理也适用于实际运动。如果只有一个物体通过场,那么,就不会有什么问题了:随着对不同的锥状细胞的相继刺激,在视网膜上引起的过程将彼此发生融合。但是,如果两个相等物体以不同方向通过场,并且同时通过同一个点,那么,“选择”的问题便又重新产生。有三种调查对这一问题进行过探索,前两种调查由特纳斯和冯·席勒(Ternnsand
Von Schiller)用断续运动进行,第三种调查则由梅茨格(1934年)用实际运动进行。
特纳斯的实验
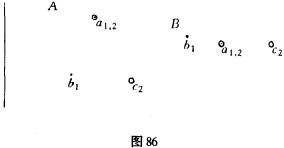
为了介绍特纳斯的问题,我们来比较一下两种简单的断续实验。在这两种实验中,每一次展现由两个点组成,致使其中一个点(即a点)在两次展现中均出现在同一地点,而另一个点则出现在不同地点(分别在b和c处)。由此可见,在两次展现中,第一次为小,第二次为ac。两次展现之间的唯一差别在于三个点的安排,如图86的A和B所示,其中●表示第一次展现,○表示第二次展现,⊙表明这一事实,即一个点在同样位置上展现两次。在A图中,我们看到a处于静止状态,而另一个点则从b向C的位置移动。然而,在B图中,情况则不同了,可以看到,没有一个点处于静止状态,两个点均处在运动之中,一个点从b向a移动,另一个点从a向c移动。由此可见,在第一种情形里,融合在出现于同一地点(a)的两个兴奋之间发生,并在出现于不同地点的两个其他兴奋之间发生,而在B图中,出现于同样地点(a)的一些过程并不融合,相反,a1与c2融合,a2与b1融合。由此可见,融合必须依赖其他因素,而不仅仅依赖空间的接近性(空间的同一性被认为是最有可能接近的例子)。那么,这里所指的其他因素究竟是什么呢?“现象同一性主要由格式塔同一性(gestalt
identity)所决定,由各部分的格式塔同源性(gestalt
homology)所决定,也就是说,由整体特性而不是由部分关系所决定”(特纳斯,p.101)。让我们通过我们自己的两个实验来对这种主张进行解释。在第一个实验中,即图A中,a通常作为一个摆的支点而出现;因此,a1和a2是格式塔同源的,与此相似的是,b和c也是同源的,因为它们作为摆臂的两个终端点。可是,另一方面,在B图中,a1是一对点子的右点,a2是左点,因此a1和a2不是同源的,a1与a2同源,a2与b1同源。当a2在第一个实验中出现时,它选择了过程a1来进行融合(a1是出现于同样地点的),但是,当a2在第二个实验中出现时,它并不选择“同源”(Syntopic)过程a1,而是选择了同源过程b1。

部分的同源性(它在质的方面也可能取代空间的同源性)并未详尽无遗地包容特纳斯概括的要义。其他的组织因素加入进来了。从特纳斯研究的各种例证中,我仅仅报道一个例证,这是由图87的A和B所表明的例证。在图87A中,融合的发生是与d、e、f各点的一致性位置相背的,而在图B中,这些一致点(d、e、f)便融合了,而且c1与g2融合,b1与b2融合,a1与i2融合。在图A中,人们可以看到一条曲线作为整体而移动,并在它自己的曲线中向右方移动,在图B中,人们可以看到一个静止的水平臂(d、e、f)和一个倾斜臂,该倾斜臂从一个位置向另一个位置跳跃。就各点的同源性而言,两种图形实际上是相等的;在第一次展现时,左边端点是a,在第二次展现时,则是d,如此等等。但是,在其他方面,这两种图形又是不同的。在图A中,由于六个同时可见的点一致地结合起来,而它们在图B中却有两个独特的点,也就是d和f那里的图形十分清晰,从而可以一分为二。与此同时,正因为这些特性,图A中的六个点可以从它们的第一位置向第二位置移动,而使整个曲线的形状不发生任何变化,可是在图B中,虚线只有通过暂时的变形做到这一点。因此,与空间同一性相背的具有选择作用的单一运动发生在图A里面,而不是发生在图B里面,后者的整个图形分裂为两部分。
冯·席勒的实验

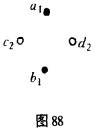
冯·席勒对选择问题进行了实验,但不区分空间上一致的和不同的展现。他从下述事实出发,即许多刺激群集在接着发生的运动方是高度两可的。于是,图88既可导致两个垂直。顺时针方向的旋转,又可导致逆时针方向的旋转。迄今为止,这种两可性已使若干作者得出结论,即视觉运动从本质上说是任意的和不可预示的,它是一种心理定势或态度,刺激模式只具次级的重要性。冯·席勒用潜在的两可图形批驳了这种观点,并证明组织因素决定了选择。根据与图88类似的一种图形,他引入了各种修改方式,借此改变了展现图形的距离。性质和形状,以及整个安排的模式。他发现同样的定律也对断续运动的选择起作用(而这种断续运动的选择是威特海默在研究静态组织时发现的)。他论证了接近因素和等同因素,并且表明,明度的差异比色彩的差异更加有效,这一结果为我们的发现(即明度差异比单纯的色彩差异具有更强的组织力量)增加了新的论据。在这些实验中,等同性因素具有特殊的意义。假设一下,在图88中,点子a1和d2都为深蓝色,b1和c2都为浅红色。如果运动遵循着等同性因素的话,那么,在运动期间蓝点保持蓝色而红点保持红色,如果断续运动以逆时针方向发生,那么蓝点将变成红色,红点则变成蓝色。这涉及整个图形的变化,而一些图形则抗拒这种变化。于是,等同性可能产生与接近因素相反的一种运动,而且,要是使用的等同性方面(颜色、明度、大小和形状)的数目越大的话,这种运动将会越强烈。在极端的情况下,甚至当十字形交叉的一些线条彼此位于15度角时,方向也可能遵循着等同性,结果,运动通过一个75度角而产生,较小角度的巨大优越性为等同性因素所过度地补偿了。这种对变化的抗拒,加上最短的路径因素,在适当条件下导致三维运动的产生。如果人们将图89的两个形状交替地加以展现,那么,最经常看到的运动便是通过第三维度绕着对称的水平轴的一种旋转运动,较少看到的运动是绕着垂直轴的图形平面运动,十分罕见的运动是一种下一上一下的运动,并在运动期间产生形状的歪曲[施泰尼希(Steining),冯·席勒]。最后一个定律是与接着通过的路径相关的;使整个途径(一切运动部分的途径)尽可能变得简单和形状化的倾向可在该因素与等同因素发生冲突的情形中得到证明。
梅茨格的实验
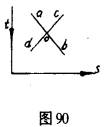
单凭这一简短的归纳,我们无法对梅茨格的系统研究进行充分的和适当的陈述。梅茨格的系统研究考察了下列情况:两个或更多的运动物体同时经过同一个点。在他的大多数实验中,运动物体是一些垂直的影子,这些垂直的影子是由插在旋转圆盘中的一些垂直杆产生的,它们经历一定距离沿水平方向前后运动。通过改变杆子以及杆子与圆盘中心之间距离的角度,他改变了那些移动的影子的状态和速度。这个问题若在图90的帮助之下可以得到最佳的叙述。在图90中,横座标代表空间距离,纵座标(向下读)代表时间。于是,该图代表两个点,其中一个点从左到右以均匀速度移动,另一个点则从右到左以同样速度移动,两个点在其轨道的中点相遇,这个中点是O。当两个点通过O点时,只有一个视网膜点(在每只眼睛里面)受到刺激;在此之前和在此以后,则两个点均受到刺激。无疑,观察者应当看到两个点的直线运动。当我们把这个图形视作空间图形时,我们确实一眼就会看到两根线相互交叉;a和b、c和d将归属在一起。然而,我们又无法看到两个直角彼此之间在它们的角项处相接触,致使a和b归属在一起,b和c归属在一起(其他的结合,ac和bd,则可以不予考虑,因为在运动中可能没有平行现象,只有运动轨迹的相继部分可以形成一个完整轨迹的一部分)。对于我们同时知觉这种空间图形来说是正确的东西,对于运动的知觉来说也同样可能:视网膜几何学并不包含这样的因素,即把ad是一个轨迹,cd是另一个轨迹的事实排除在外的因素。但是,在运动中,还存在着更多的可能性。由于在O点只有一点受到刺激,因此这种刺激模式也可能与下列情况共存,即两个点(或者两个点中的任何一个点)都在O点上消失,并且有两个新的点从O点上冒出来。有否定律去决定实际上发生的事呢?
梅茨格的主要结果能以下列方式进行阐述:如果有人运用图90的图解产生的运动并加以描绘的话,那么,当我们注视该图形时所出现的或占支配地位的空间模式通常与我们注视着运动影子时出现的或占支配地位的运动模式是一样的。这就意味着:相继组织定律(也就是决定融合物体选择的定律)与支配空间模式之组织的定律是同样的。梅茨格十分明确地陈述了这种一致性。我们仅仅提及一点:与纯空间组织中良好的连续因素相一致的有运动的平稳曲线因素,以及空间-时间组织中的连续速度因素。
显然,情况可能是这样的:不同的因素有利于不同的结合。这些客观因素之间的冲突越大,模糊性便越大,从而使定势和态度等主观因素的影响也越大。上述这种结果,对于特纳斯、冯·席勒和梅茨格等人的研究来说是共同的。它表明了有一种观点是何等地错误,这种观点认为,主观因素在引起运动过程方面是首要的(见边码p.33)。梅茨格有一论点令人注目地表明了这种观点的荒谬性。运动的可能轨迹数随物体数和旋转周期数而急剧地增加。于是,在他的圆盘上,根据圆盘上杆子的安排,10根杆子在半个循环周期中提供了最少为
3628800个可能性,而最大的可能性为35184372088832。对于一个完整的旋转周期来说,最大值是 1.2 X 1027。梅茨格的被试在大量的旋转期间偶尔观察到10个成员以上的群体,然而至多只能意识到少数不同的运动轨迹。
空间和感觉道
在我们从上述的研究中了解了威特海默的组织定律的意义之后,我们还从加利(Galli)的一项研究中获得了对知觉到的空间性质的一种新的顿悟。在断续运动中,一种过程与另一种过程相融合,甚至当两种过程在颜色、大小和形状方面不同时,也会发生融合。但是,在迄今为止报道的一切实验中,断续地呈现的不同物体均属于同样的感觉道(sense
modalities),它们都是视觉物体,先前已经提及,它们也可以是听觉的或触觉的物体。但是,如果两个相继呈现的物体属于不同的感觉道,例如光和声音的结合,或者光和触觉的结合,将会发生什么事呢?如果视觉、触觉和听觉是三种不同的空间,仅仅由经验把它们联系在一起,那么,这种呈现就不会导致运动的印象,这是因为,按照我们的理论,这种印象意味着同一个心物过程通过(同一个)空间。因此,如果断续运动可以由不同感觉道的印象产生的话,那么,根据我们的理论,我们必须得出结论说,知觉空间是一个可以由不同感觉道的物体所填充的空间。有关的实验就是用来研究第二种选择的。加利通过把两种或三种刺激结合起来的方式(它们属于视觉、听觉和触觉道)来产生断续运动。被试多次体验一个运动着的物体的运动,该运动物体以木同方式对“被试产生影响”。这些实验使动态运动和知觉空间结构更清楚地显示出来。
关于行为物体之性质的结论
在我们结束本章以前,我们将评价一下有关物体研究的结果。在我们关于知觉场的整个讨论中,物体和格局的区分已被证明是最基本的。在第三章里,我们确立了事物的三种主要特性,也就是说,形状的界限、动力特性和恒常性。对于这三种主要特性来说,第一种已经在第四章详尽而充分地探讨过了,因此,对此论点毋须详述。然而,本章将其他两种特性的大量知识汇集到一起。事实上,由于这两种特性彼此之间密切联系,所以能够结合起来探讨。根据这些方面的观点,人们试图对我们的先前讨论冒险作出下列概括:对于一种刺激的变化所作的反应会使事物尽可能地保持它们的特性。在运动领域,我们发现这一原理是起作用的;过程和路径的融合倾向于如条件许可的那样将事物保持原封不动。该情形的一个方面是我们转动眼睛时事物的稳定性,这是因为,在该情形里,视网膜意像的形状是始终变化的,然而,事物却不改变它们的形状。同样的效应也为形状和大小恒常性所表明。旋转一个物体,改变它的视网膜意像,所见事物的形状将保持相对地不变,而视网膜意像的变化由方向的改变所引起。对大小和距离的应用是简单的。甚至明度和颜色恒常性也归入同一规律之下:客观照明的改变主要引起知觉到的明度(或亮度)的改变,而不是知觉到的物体的颜色特性的改变。
加利通过把两种或三种刺激结合起来的方式(它们属于视觉、听觉和触觉道)来产生断续运动。被试多次体验一个运动着的物体的运动,该运动物体以不同方式对“被试产生影响”。这些实验使动态运动和知觉空间结构更清楚地显示出来。
我们的理论不仅回避了这一点,而且,与此同时还避免了德国哲学家康德的先验论(Kantian apriorism)。
小结
在前面几章,我们试图对下列框架进行填充,这个框架是由我们对这样一个问题的最终回答来提供的:为什么事物像看上去的那样?我们已经对组织进行了多方面研究,得出了一种知觉理论,尽管它还十分不完整。与此同时,我们也试图对我们的组织含义进行描述,对我们的理论目的和方法予以洞察。在这个意义上说,这几章为后面几章充当了导言的角色,在后面几章里,我们将扩大我们的研究范围。但是,在我们即将研究的广泛范围内,我们仍然受制于同样的方法论原则,并且,仍想发现在我们的讨论中建立起来的“组织定律”(laws
of organization)的巨大力量。 |