首页 -> 2008年第7期
浅谈数学思维的创造性的意义及其培养
作者：曾 坤
[关键词]思维的创造性 素质教育 思维训练 培养
（一）思维的创造性是思维品质的重要特征之一
思维的创造性是指思维活动的创造精神，是在新颖地解决问题中表现出来的智力品质。它是个体在强烈的适新意识的指导下把头脑中已有的信息重新组合，产生的具有进步意义的新设想和新发现。它不同于传统的旧模式，与老师平时讲的内容、教材内容完全不同。这种思维特征具体表现在学生学习数学过程中，突然发现老师所讲例题的其他一些解法，发现教材定理的另外证明方法等。从某种意义上说，数学创造性思维是在可供选择的各种解决问题的方案中，找出最优解决方案的思维过程。
（二）思维创造性的培养是实施素质教育的需要
当今，知识技术正以无比巨大的力量改造着我们周围的一切。社会对人才素质的要求越来越高。时代要求我们培养的人才，应具有善于发现问题、并能提出独到的、有效的解决方法的能力。
1.思维创造性有利于优化人的综合素质。人的综合素质包括注意力、观察力、记忆力、理解力、想象力等因素。创造性思维正是这些因素的有效综合，因而它促进智力因素和非智力因素共同发展。
2.通过创造性思维训练，能促进人的大脑的协调发展，让人的潜能得到充分发掘。
3.创造性思维的培养有利于促进人的个性发展。创造性思维的本质是新、是独特、是与众不同，而我们教育的目的之一就是要培养具有个性化的创造型人才。
（三）在中学数学教学中如何培养学生思维的创造性
1.通过培养学生完备合理的知识结构来形成和发展创造性思维。一位数学家曾指出，数学发明创造是识别、是选择、是知识的重新组合。因此，我们讲合理的知识结构有利于学生的新知识的同化，有利于创造性思维的形成与发展。要在提高学生的解决问题能力方面有所突破、有所创新，就必须使学生的知识结构、认知体系合理化、科学化并具有系统性。只有当学生头脑中的认知结构合理化，才能达到思维方式的科学，进而创造性地应用知识去解决问题。
2.通过创设自由愉快的学习情境来促进创造性思维的发展。数学情境能唤起学生的问题意识、参与意识、合作意识，使学生在情境中产生好奇、渴求、探索的欲望，不断去提出问题、探究问题和解决问题。老师应尽力创造一种良好的学习气氛，让学生敢于去想象、敢于去质疑、敢于去标新立异，进而积极主动地去发展和学习。这种自由愉快的学习情境，有利于培养学生创造性学习的心理品质。
在教学过程中可以创设以下三种情境：一是可以结合教学内容创设一定的故事情境，让学生在情境中产生兴趣，积极参与到教学活动中来；二是可以创设实验情境，使抽象知识具体化，让学生在观察、分析的过程中茅塞顿开、情绪倍增；三是可以创设问题化情境，使学生在发现问题、分析问题和解决问题的过程中，让思维处于活跃状态，随时可获得灵感。
3.通过搞活数学思维训练，启发创新意识来培养创造性思维。在数学教学中，可根据数学教材的特点和学生的心理特征，有计划地开展对学生数学思维的训练。在搞活思维训练时，可考虑从以下三个方面着手训练：
（1）发散性思维训练。发散性思维主要培养学生从多角度、多层次、多渠道去观察和分析问题。数学上的新思想、新概念和新方法往往来源于发散思维，它是创造性思维的重要成份。在数学教学中，为防止思维程式化，对于一些问题，尽可能变化为已知条件，从不同的角度用不同的知识来解决问题。这样既可以揭示数学问题的层次，又可以充分暴露学生自身的思维层次，让学生从中吸取数学知识的营养。
（2）开拓性思维训练。创造性思维的一个特点是能开拓出不同于一般的有效解题方法。为此，必须多思善断，对概念要一义多析，对试题要一算多法，对应用题要一题多变和多解。例如，当m为何值时，直线x-y+m=0被曲线x2+y2=5所截得的线段之长为
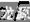？按照平常习惯的思路来解这道题，是将直线方程代入曲线方程，求出它们的交点坐标，再借助韦达定理和距离公式来解。但这样比较麻烦，如果我们再仔细分析一下本题所给的条件具有新的特点：曲线是圆，圆的半径为
，直线x-y+m=0被圆截得的弦长为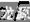，即为圆的直径。于是，直线x-y+m=0必须通过圆心，所以m=0。
（3）形象思维训练。在数学教学中，培养学生多角度、多侧面地进行形象思维的习惯，是提高学生学习能力的重要手段之一。形象思维所起作用明显地表现在图形上。如果我们能够把某个特定的问题转化为图形，那么我们从思想上就整体地把握了问题，并且能创造性地思索问题的解法。
以上从三个方面谈了培养创造性思维的方法，这些方法不是孤立的，而是相互渗透、相互促进的。我们要激励学生灵活地运用培养创造性思维的各种方法，把创造性思维品质与一般性思维的品质有机地结合起来，做到有目的、有计划地加以训练和培养。
参考文献：
[1]田万海.数学教育学[M].杭州:浙江教育出版社,1993.