首页 -> 2007年第10期
利用凯塞窗函数法设计的ＦＩＲ数字滤波器与仿真
作者：陈 鹏 杨理践 刘佳欣
[关键词]凯塞窗 FIR MATLAB 数字带通滤波器
所谓数字滤波器就是具有某种选择性的器件、网络或以计算机硬件支持的计算程序。其功能性质是按事先设计好的程序，将一组输入的数字序列通过一定的运算后转变为另一组输出的数字序列。从而改变信号的形式和内容，达到对信号加工或滤波以符合技术指标的要求。
(一)FIR滤波器介绍
1．FIR滤波器设计的原理。
FIR滤波器的数学表达式可用差分方程(1)来表示：
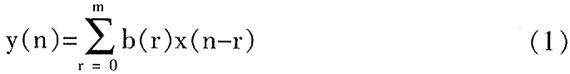
其中：x是FIR的滤波器的抽头数；b(r)是第r级抽头数(单位脉冲响应)；x(n-r)是延时r个抽头的输入信号。
设计滤波器的任务就是寻求一个因果，物理上可实现的系统函数H(z)，使其频率响应H(ejw)满足所希望得到的频域指标。
2．设计要求。
本次设计中输入数据中包含频率为800Hz，1200Hz，1600Hz，2021Hz，中心频率为1600Hz，提取该频率的信号。利用MATLAB设计一个带通滤波器。具体参数为：采样频率为22050Hz，通带宽度为250Hz，则Fpassl=1475Hz，Fpass2=1725Hz，衰减1dB，过渡带为200Hz，则Fstopl：1275Hz，Fstop2=1925Hz，阻滞衰减为30dB。运行MATLAB获得126阶的带通滤波器。并提取系数。
(二)凯塞窗函数的介绍
在设计FIR滤波器中，一个最重要的计算就是加窗，Kaiser窗可以通过调整参数值来折中选择主辦宽度和旁辦衰减，采用Kaiser窗设计FIR滤波器具有很大的灵活性。
凯塞窗是一种适应性较强且比较灵活的窗函数，它的表达式为：
这种窗函数是近似于给定旁辦电平，使主辦具有最大能量意义下的最佳窗函数。其中β是形状参数，用以调节主辦宽度和旁辦电平，一般β选为4＜β＜9，此时旁辦电平约在30dB和-67dB之间。
(当β=5.44时，接近汉明；β=8.5，接近布莱克曼；β=0，为矩形。)
(三)Simulator仿真结果分析与硬件调试
在本次设计中利用CCS提供的断点和探测点，同时利用CCS提供的图形窗口观察输入和输出的波形与频谱。运行程序，分别得到输入波形和频谱图(图一)，输出波形和频谱图(图二)。下面分别对这两个图形进行分析。
由图一输入信号的波形图可以看出。输入是有四个不同频率调制的波形。左边第一种图形在一个周期内占大约l格。而一格所占的时间为3.00605/10=0.605ms，所以周期大约为T1=0.605×1=0.605ms，频率为1652Hz。最右边的图形一个周期内约占0.8格，T2=0.605×0.8=0.484ms，频率约为2066Hz。中间的两个图形在一个周期内分别约占2格和1.3格，周期分别约为T3=0.605×2=1.21ms，频率约为826Hz，T4=0.605×1.30.7865ms，频率约为1271Hz。这四个频率与输入的800Hz，1200Hz，1600Hz，2021Hz基本相同。
由图二中的输出信号波形图可以看出滤出的波形在一个周期中约占l格，而一格所占的时间3.00605/10=0.605ms。频率约为1652Hz，与要求滤出1600Hz的要求接近。
基于上面结果，利用TMS320C5402DSK系统板实验，在一个AD/DA转换的主循环中加入所设计的滤波器，对示波器进行观察，可以发现所用的滤波器能很好的满足设计要求。