首页 -> 2007年第10期

浅谈行列式的计算方法

作者：田立霞

　　在线性代数中，行列式是一个重要的基本工具，因此熟练地掌握行列式的计算方法是非常重要的。下面结合几年来的教学实践，谈谈计算行列式的常用方法。
　　
　　(一)定义法
　　
　　即把行列式按第一行进行展开，其值等于该行所有元素与其相应的代数余子式乘积之和而得到，请看：
　　
　　通过此题的计算，我们体会到第一行的零元素越多，按第一行展开时，计算就越简便。
　　
　　(二)三角形法
　　
　　这是计算行列式的一种基本方法。它是把一个行列式通过行列式的性质，设法把它们化为三角形行列式，然后求其值。请看：
　　
　　方法：把第一行乘以(－1)分别加到第2行、第3行、……、第n行，然后再按第一列进行展开。
　　
　　从本例可以看出，如果在一个行列式中，位于主对角线上(下)边各个元素与第1行(或)列中，同列(或)行的元素都相同或互为相反数，那么把它化为三角形行列式将是较为方便的。
　　
　　(三)降阶法
　　
　　即利用行列式的有关理论降低行列式的阶数，然后计算行列式。
　　
　　方法：因第3行只有一个元素不是零，故按这一行进行展开。
　　
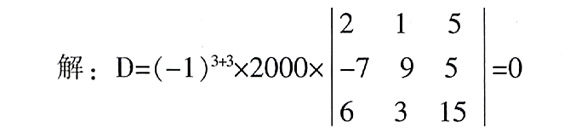
　　(1行、3行对应元素成比例)
　　
　　(四)拆开法
　　
　　如果行列式的某些行(或)列的元素有规律地表示为两项的和，就可以把该行列式拆开为两个行列式之和，然后再进行计算。
　　
　　
　　此外，还有递推法、利用反对称行列式的性质来计算行列式的方法，本文暂不做阐释。
　　从以上我们介绍的几种计算行列式的方法中，我们可以清楚地看到，许多方法不是单独使用的，这就要求我们要仔细观察行列式的结构，以找出切实可行的办法来达到快速、准确、方便地计算行列式。