首页 -> 2008年第11期
浅析利用信息技术培养学生的数理结合能力
作者:查冲平 张桂琴 陈光学
例:设工件内表面的截线为抛物线y=ax2+bx+c,现在要用砂轮磨削其内表面,问用半径多大的砂轮才比较合适?
解答:本问题涉及物理、数学、机械工艺等知识。例如,凹透镜、凹面镜的焦点问题是光学知识,利用它们可得到平行光;制作凹透镜、凹面镜并用砂轮磨削其内表面是机械工艺问题;而寻找合适的砂轮却需要数学知识。因此,本例是基于物理知识(光学),从实际/物理需要(制作凹透镜、凹面镜)出发,利用数学知识(寻找砂轮)来解决生产技术问题的现实例子,正确解答本例有利于培养学生的数理结合能力。
本例中,为了磨削时不使砂轮与工件接触处附近的那部分被磨去太多,砂轮的半径应不大于抛物线上各点处曲率半径的最小值。为了让学生对这一问题有一直观的了解,我们制作了下图来模拟,这也是本问题的数学抽象。
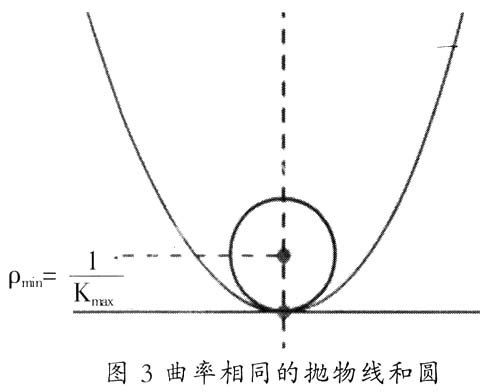
通过该图,学生能对欲解决的问题有一个直观的印象(而解决本问题的意义,如得到凹透镜、凹面镜的焦点等,是以物理上的光学知识为基础的)。接下来就是如何把这个问题转换为数学模型。为了能正确地将该问题转换为数学问题,学生首先必须知道曲率、抛物线与圆的曲率中心及曲率半径的数学知识,一旦学生认识到抛物线最低点的曲率半径与圆的半径相等时,该圆形物体就能摩擦到此工件最低点这一知识时,本问题就能得到解决。接下来的问题是数学求解,即先求出抛物线的曲率半径,即:
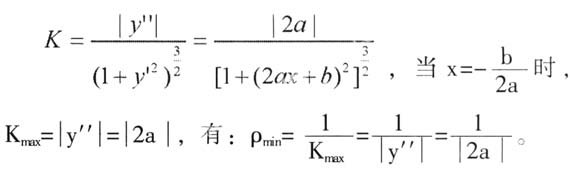
最后剩下一个问题,即利用计算出来的数学结果去解释该物理问题。由结果可知,所选择的圆形砂轮的半径只与抛物线方程的参数a有关,而该参数表示的是抛物线的开口的,即所选圆形砂轮的半径仅与抛物线的开口有关,这与实际生活中人们的印象也是相符的。
在该例中,利用可视化的方法来培养学生的数理能力,主要体现在将物理问题形象化上面;另外一个突出的作用是,利用图形,学生从圆形与抛物线相接的地方,容易想象到二段曲线的拟合,从而能进一步想象出如何让二段曲线拟合起来,即曲率相同,这样自然得出用曲率的数学知识来解决问题;另外,还可以绘制不同开口的图形,这样学生能看到将出现不同大小的砂轮,从而加深他们对该物理问题的印象,同时加深了对计算结果的理解与记忆。这样,也达到了对他们数理结合能力培养的目的。
恰当地使用合适的信息技术手段,不光对培养学生的数理结合能力有帮助,对学生物理、数学知识的深入掌握,也是有帮助的。在我们的教学实践中,就收到了良好的效果。使课题组成员印象深刻的是y=x2的函数图形,当学生第一次看到计算机绘制的图形和他们平时手工绘制的图形的差别(开口大小)时,学生都发出了感叹的声音。我们认为,信息技术取得了预期的效果。
数理结合能力对于本科物理专业的学生是一项必备技能,是他们进入物理研究的必经之路。如何培养他们的数理结合能力,除了在教材选取、教学方法转变等常规途径上加强或改革以外,利用信息技术来培养这方面的能力也应该纳入数理结合能力培养系统工程中来。信息技术的发展已渗透到社会的方方面面,教育信息化是各国教育改革的方向之一,它体现在教育的各个层面。我们利用信息技术来培养学生的数理结合能力,是教育改革与培养学生数学、物理知识的客观要求。在我们提到的这些方法中,是对该领域的尝试实践,实乃抛砖引玉,我们将在今后的工作就此问题做进一步深层次的研究。
[1]