首页 -> 2008年第11期
数学课堂教学中如何培养学生的创新能力
作者:赵春雨
一、兴趣是培养和发展学生创新能力的前提
教育学家乌申斯基曾经说过:没有丝毫兴趣的学习,将会扼杀学生探求真理的欲望。所以,兴趣是学习的重要动力,也是创新的前提条件,创新的过程需要兴趣来维持。
1. 利用学生渴求问题的心理,培养学生的创新兴趣
在教学中出示难易适度的问题,让学生“跳跳脚,就能摸得着”。这样的问题会吸引学生,可以激发学生的认知矛盾,引发学生强烈的兴趣和求知欲,学生因兴趣而学习和思考,并提出新质疑,自觉地去解决、去创新。
2. 利用学生的好奇心和好胜心,培养学生的创新兴趣
学生都有强烈的好胜心理,如果在学习中屡屡失败,会对学习失去信心,所以教师应该创造合适的机会,发挥它们不同的特长,在活动中充分展示自我,找到生活与数学的结合点, 使学生感觉成功的喜悦。
3. 借助数学与现实生活中的联系,培养学生的学习兴趣
在现实生活中,大量的实物是产生几何图形的原形,有的是根据数学中的重要理论产生的,也有的是几何图形的组合,它们具有很强的审美价值。
例:如图所示,有六种图形
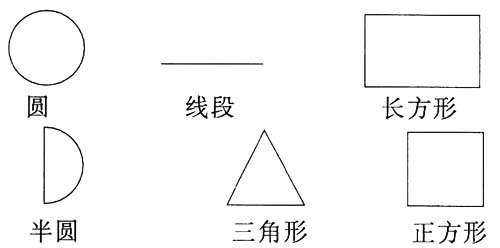
请你用六种图形的若干种(不少于两种,每种图形可重复使用)构造一幅图画,并用一句话说明你构想的是什么?
学生们展示自己的思维想象能力,创作出火车、雪人、蘑菇、太阳、小鸟、蜡烛等等,充分发挥了学生的想像力、创造力。
所以在教学中应尽量把生活实际中美的图形联系到课堂教学中,再把图形运用到各种创作设计中,产生共鸣,使他们产生创造图形美的欲望,驱使他们创新,维持长久的创新兴趣。
二、学生创造性思维能力是创新能力的核心
新课标教学注重培养学生的创新性思维,因此,在探究过程中,要提倡思维方式的新、奇、活,具体做法有:
(1) 让学生在“猜想”中学习新奇的思维方式,只要学习内容能反映出数学的发展过程,就引导学生大胆、合理地进行猜测、假设,提出一些预感性的想法,实现对事物的瞬间顿悟。
(2) 让学生在变通中学习巧、活的思维方式。训练学生由正及反、由此及彼、举一反三的迁移变通能力。
例如,在讲解应用题时,尽量让学生能一题多解,或者把原题改题、编题。变题等于灵活变通,从而增强学生对新知识的理解程度和探索新知识的兴趣,这个过程不仅训练了学生的直觉思维和简单的逻辑思维能力,也培养了学生对事物认识的独创性和跳跃性思维品质。
(3) 让学生在“求异”中学习多、优的思维方式,使学生在求异中不断获得解决问题的多种方法,并逐步趋向优化。例如:在求代数式值时,通过学习,让学生总结得出:①将字母的值直接代入求值。②先化简代数式,再代入字母的值求值。③已知或代数式变形,再整体代入求代数式的值。
三、实验是培养学生创新能力的最佳途径
动手操作实践以其生动、直观、新异、有趣等特点,对学生有很大的吸引力。它不仅能培养学生的创新观察能力和创新实践能力,还能培养学生的创新思维能力,是培养学生创新能力的关键环节。因此,教师要善于组织学生亲自动手操作,在实践过程中要求学生仔细观察,通过教师引导,从观察到的现象中去发现问题,解决问题,总结规律。例如:在研究《哪些平面图形是正方体的表面展开图》一节中,刚刚入学的七年级学生学习非常困难,我是这样做的:首先要求学生用网格纸剪出所给的平面图形后,师生共同演示,用手去折叠,看能否折成正方体,然后对能折成正方体的平面图形,观察其特点,能找到三组对面(找对面的方法①相间型

1和4对面。)最后总结有6个相同正方形构成的平面图形,如果有三组对面,则该平面图形一定是正方体的表面展开图。
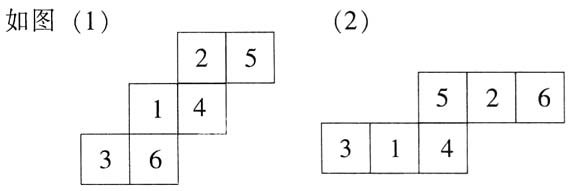
说明:图(1)或(2)中,1和2对面,5和6对面,3和4对面,都能折叠成正方体,是正方体的表面展开图。通过学生亲自操作,找到了解决难点的方法,即“找三组对面法”,从而使学生对11种正方体的表面展开图很容易判断,这样做也培养了学生动手动脑的创造能力。另外,对学生的小制作、小发明,要经常表扬学生的劳动成果,从而激发学生的创造发明欲望,提高学生的动手操作能力。
总之,创新能力的实质就是求新、求异,新课标数学蕴含着丰富的创新教育素材,数学教师要根据数学的规律和特点,想方设法为学生提供各种机会,努力寻找培养和发展学生创新能力的有效途径,重视开发学生的创新潜能。