首页 -> 2008年第10期
在小学数学教学中渗透对应思想
作者:王立芳
一、在数数中渗透对应思想
10以内数的认识的教学,就是利用了等价集合一一对应思想。教学中采用直观形象的方式,借助于图形,通过物与物、物与形的对应,由数数过渡到认识自然数。在数数时,实质是先要对实物进行分类,把每一类看作一个集合,然后依次指着集合中的每一个元素,分别同自然数中的1、2、3……对应,直到最后的一个元素,同它对应的自然数就是这个集合中元素的个数,也就是物体的总数。例如,由两个小朋友、两只飞机模型、两只小鸟等等价集合的对应,过渡到与数“2”的对应等等,都渗透了物与物、数与物之间的对应关系。
二、在计算教学中渗透对应思想
教材中计算教学对应思想是通过方框图(或韦恩图),结合具体运算进行渗透的。例如:
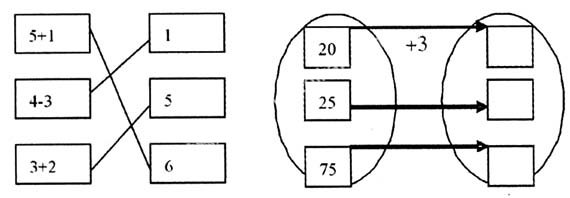
栏式题右边的方框里的数,是这栏式题的得数,把每道题和它的得数用线段连起来。通过这种练习可以复习已学的加减法。
有时,数与数的对应关系,还通过列表的方式加以体现。例如:

这样做,既渗透了数与算式,算式与算式之间的对应关系,又改变了过去教材中计算题的题型单调的不足之处。
三、在序数(数的顺序)教学以及分数教学中渗透对应思想
(1)在()中填上适当的数
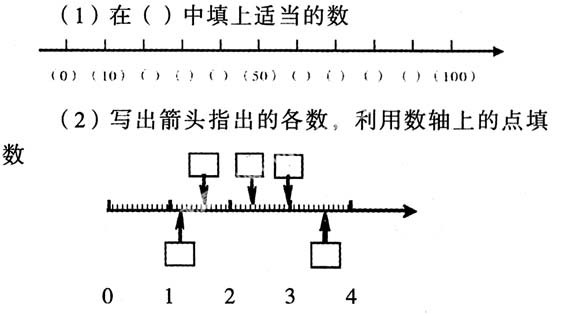
这里渗透了整数、小数集合中的数与数轴上的点是一一对应的,为以后进一步学习数轴上的点与实数是一一对应的埋下伏笔。
四、在认识图形中渗透对应思想
在第一册“认识图形”中,教材中的“做一做”要求学生把形状是长方体、正方体、圆柱和球的物体用线分别与长方体、正方体、圆柱和球的立体图形连起来。这里要求学生把实物和它所对应的几何图形用线连起来,目的是帮助学生辨认所学的几何形体。
五、在应用题教学中渗透对应思想
解答应用题必须分析数量关系,应用题的数量关系,实质为量与量之间的对应关系。
例如,学校养了12只白兔,7只黑兔,白兔比黑兔多几只?
对于低年级学生来说,刚接触应用题,为了使学生明白谁多谁少的含义,可以画出实物图。比如,用黑圈表示黑兔,白圈表示白兔,则可进行形象、直观的对比。

使一只黑兔对着一只白兔,一一对应的部分是同样多的部分,学生会发现,有5只白兔没有黑兔与它们对应,由此启发学生理解白兔比黑兔多的含义。
对于典型应用题来说,经过多次的实践、抽象与概括,量与量的对应关系上升为公式。例如行程问题中的“速度×时间=路程”,求平均数问题中的“总数量÷总份数=平均数”等等,都是以公式形式出现的量与量之间的对应关系。在分析应用题的数量关系的过程中,常常把已知条件、要求的问题,对应为表格或者图形,采用数形结合的方式进行分析。
对于分数应用题,抓准分率与实际的量的对应关系是解答的关键。分数应用题的数量关系比较抽象,必须充分利用半具体半抽象的线段图作为解题工具。通过分析线段图,明确谁是单位“1”,谁是对应分率,它可以帮助学生在复杂的条件和问题中,理清思路,找到解题线索,有利于发展学生的逻辑思维能力。例如:小青看一本书,第一天看的页数比总页数的1/8多16页,第二天看的页数比总页数的1/6少2页,还余下88页,这本书共有多少页?
审题,画线段图,说明题意,进行分析:
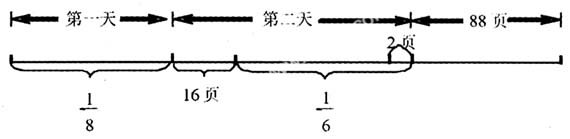
显然,分率(1-1/8-1/6)对应的页数为(88+16-2)。所以,这本书的总页数是(88+16-2)÷(1-1/8-1/6)=144(页)
学生有了对应思想,掌握了对应的思想方法,无论应用题的条件如何变化,都能认清应用题的量与率的对应关系,找到解决问题的途径与方法 ,以不变应万变。
只有让学生从小接触到数学的对应思想,才能在以后的数学学习和数学应用中,熟练应用对应思想,提高学生分析解答应用题的能力,使学生在生活中熟练应用对应思想,运用数学知识,解决实际问题,真正让数学回到学生身边,让数学与生活完美结合。