首页 -> 2008年第6期
运用“操作—猜想”提高数学教学质量
作者:陈荣玲 赵庆丽
猜想是对研究的对象或问题进行观察、实验、分析、比较、联想、类比、归纳等,依据已有的材料知识作出符合一定的经验与事实的推测性想象的思维方法。心理学家皮亚杰认为“思维是从动作开始的,切断了动作思维之间的联系,思维就得不到发展”。因此需要将猜想与动手操作有机的结合起来。
一、“操作—猜想”促进直觉思维
初中数学中的许多概念、性质、判定等知识,对于正处于由感性认识到理性认识转化的初中生而言是比较抽象的。让它们通过观察具体图形或实物模型和动手实验,根据自己的观察实验,在感性认知的基础上提出合理的猜想,对加深学生认知与促进学生的直觉思维是相当有益处的。
例如,教师在讲授“等腰三角形的两个底角相等时”,教师可先让学生拿出已准备好的等腰三角形纸片,引导学生进行观察并对两个底角的关系进行猜想。学生通过自己的感官反应马上得到“等腰三角形的两个底角相等”,在教师的肯定与赞扬声中,学生们跃跃欲试,又通过动手操作:有的拿出了量角器来进行测量,有的通过对折来看这两个角能否重合……很快他们就找到了验证自己猜想的方法,并自然而又深刻地掌握了这一性质。
又如新授“三角形中位线”定理时,学生们在了解了“连结三角形两边中点的线段是三角形的中位线”之后,通过“画一画”“量一量”“看一看”的操作来猜想三角形中位线的性质,通过学生自己的观察与测量得到了“三角形的中位线平行于第三边且等于第三边的一半”,并饶有兴趣地进一步推理论证该定理。在讲授新知识的同时,让学生体验着知识本身的魅力与内心的喜怒哀乐,同时又培养他们的直觉思维能力。
二、“操作—猜想”促进数学归纳
“归纳”是数学思想和数学能力中很重要的一块,“操作—猜想”这一形式对培养学生的归纳思想与能力所起的作用更是妙不可言。例如,观察下列图形,并阅读理解图形下的有关文字。

那么n直线相交,最多有多少个交点?刚看到题目的时候,学生们有些丈二和尚摸不着头脑,于是教师可启发学生:动手画一画,用心数一数,学生在画的过程中发现:当画第二条直线时,我们发现已有直线一条,因此最多可有一个交点;当画第三条直线时,最多可与原有的两条直线相交并有两个交点,因此一共有三个交点;……渐渐地发现,直线的条数与交点的个数是两组很有规律的数据:
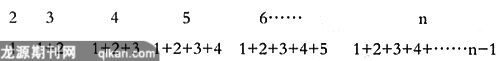
于是根据高斯定理,就可得: n条直线相交,最多可有n(n-1)/2个交点。在整个解决问题的过程中,学生从没有头绪到豁然开朗,正是操作起到了决定性的作用。初三应用题这一章节中,有一类“送礼物”、“打电话”问题的应用题。学生学习的过程中,很难把握其规律。教师在新课引入时,可创设一个游戏情境:圣诞节即将来临,希望每一位同学为其他同学准备一份礼物,请大家回去准备一下吧!这一下学生们七嘴八舌地嚷开了……这是学生生活中经常碰到的问题,他们对此很感兴趣!于是教师又抽取了四位学生进行演示:四位同学要完成送礼物任务,大家看“每一位同学要准备几份礼物,最后所有的同学将共送出几份礼物?”很快地,学生发现:每位同学要准备的礼物数比人数少1,因此如果有n个学生的话,礼物的总数可归纳为n(n-1)。通过学生亲身演示与体验,把一个比较抽象的问题具体化、可操作化,这样便于学生理解掌握。归纳思想是初中阶段重要的思想方法之一,通过操作猜想,让学生在动手过程中迸出智慧的火花,建立起猜想,从而激发进一步归纳的欲望,让自己从特殊到一般,逐步归纳出更完美的结论!
三、“操作—猜想”促成类比思维
看到“铁锹铲地”产生联想类比,从而改进了建筑工地上的抓斗机。通过操作猜想进行类比,根据两个事物之间类似或是相同的特点,猜想出它的类似或相同的规律或性质的一种数学方法。教师新授等腰梯形的性质“同一底上两个底角相等”时,完全可以启发学生回忆学习等腰三角形性质时的方法:得到等腰梯形“两个底角相等”的性质。又如,学生学习“等腰梯形中位线定理”时,学生马上会回忆起学习“三角形中位线定理”时的情形,从而促进新定理的学习。教学中让学生在“手脑并用”中体会“观察——联想——类比——猜想”的思想方法,无疑是一种行之有效的方法!
四、“操作—猜想”启发验证方法
很多时候,猜想是“跟着感觉走”的,不一定符合事实,故猜想的结果也就不一定可靠,因此不论你的猜想多么地美妙,都需经过严格地验证,才能肯定自己的猜想是否正确。例如初三复习课上,教师向学生给出了这样一道习题:设A、B、C、D是四个居民小区,现要在四形ABCD内部建立一个购物中心,试问应把购物中心健在何处,能使四个居民小区到购物中心的距离总和最小?
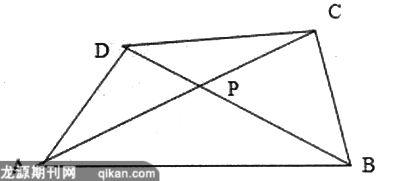
因为四边形ABCD内有无数的点,学生很难找到确切的解决途径。学生没有通过动手操作,是很难想到从特殊的点出发,再进行猜想,然后再加以论证的,学生通过动手画图,在圈圈点点中学生发现:在四边形ABCD内部的点可以分为两类。一类是在线段AC与BD上的:一类是在四个小三角形内的。逐渐的,在一次又一次的画图中,进一步证实了只有P点才是符合要求的。同时在测量中也已经发现可以利用“三角形两边之和大于第三边”来进行严密地论证。在教学过程中,注重创设“操作—猜想”情境,让初中数学课堂教学以动手操作为基础,以体验乐趣为动力,以猜想为翅膀,飞向更广阔的蓝天。鼓励学生参与学习、体验学习,从而获得成功之后的满足与愉悦。让学生们真正自主地、快乐地学习数学!