首页 -> 2007年第6期
如何帮助学生形成解决问题的策略
作者:陈 霞
一、直观策略
当问题比较抽象复杂时,可以根据题意构造直观,使问题形象化,以便发现解题的途径。教学中,教师可在学生理解题意的基础上启发学生调用原有方法和技能,把问题放在具体直观的背景中加以解决。如当学生品味到运用转化方法能从(已知)长方形面积中推得(未知)平行四边形面积公式时,要求学生通过剪拼,在独立思考中解决三角形、梯形的面积公式,实际上是进行公式的再创造。再如,面对较复杂的问题,教会学生创造直观背景——作图、列表、模拟演示等,其中最为常用的当推直观图示。例如:甲数的1/2等于乙数1/5的,甲数是乙数的的几分之几?题中已知条件较为抽象,但只要画一画直观示意图,问题就迎刃而解了。如:
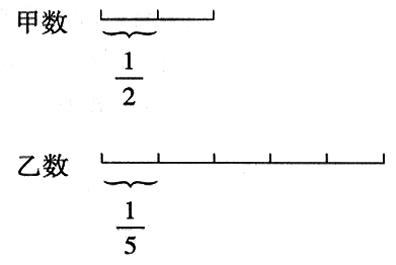
学生根据图,就很容易列出下面的算式:2÷5=2/5。由此可见,遇到复杂问题时,借助直观手段,可以使复杂问题简单化,抽象问题具体化,便于学生找到解题途径。
二、列举推理策略
列举推理是一种重要的数学思维形式,常用于概念的形成,性质、规则、公式的推导。教学时应努力使学生领会数学推理的基本思考方法。如通过对具体事例的分析比较、寻找规律、归纳结论的方法;利用已有的知识或经验,对新问题作出判断、分析,寻找问题结论的方法。前者一般用于新知识探索过程中,属于归纳推理;后者一般用于知识应用过程中,属于演绎推理。但是在其具体运用时,常常顾此失彼,考虑不全。为此,应教给学生列举推理的思考方法。如:两根同样长的绳子,第一根截去1/4米,第二根截去它的1/4,剩下的哪根长?学生往往只会考虑大于1米或等于1米的情况,其实还有小于1米的情况,要列举出三种情况,全面地进行推理,才能得到正确的结论。
为了提高列举推理的可靠程度,在教学中要求学生考察的数量尽量多一些,范围尽量广一些,尽量避免“轻率概括”,同时要指导学生搜集反面事例进行考证。
三、变式转换策略
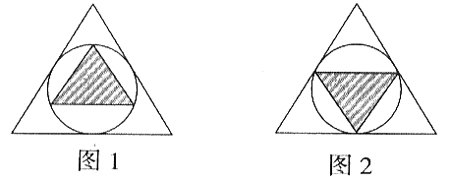
主要使学生掌握“形变积不变”、“等量代换”、“换一角度思考”等数学中经常要用到的思考方法。在解题中这些方法常常起到“柳暗花明”的效果。如:在一个正三角形内画一个最大的圆,在圆内再画一个最大的正三角形。(如下图1)已知大正三角形的面积为48平方厘米,求小正三角形的面积是多少?用图1思考,简直“疑无路”。转动小正三角形成图2时,学生顿时豁然开朗,一看便知道小正三角形的面积是大正三角形的1/4。在平时的教学中,我们可以精心设计此类问题,引导学生多角度思考,在动态变换中获取问题解决的途径,锻炼学生的数学思维能力。
四、评价策略
评价是指对问题解决过程的合理性、简捷性等因素作出评判,对解决的策略、方法进行总结。学生对学习过程和结果进行自我评价是学生学习能力的表现。
教学生评价主要使学生掌握由果索因的评价策略。由果索因,一方面引导学生把结果放置在条件中加以检测,如应用题的检测评价。另一方面还包括从结论出发、重新回忆结论形成的过程。常用的办法是指导学生自己设置条件,仿照前面结论形式过程作再推导,以评价自己对结论的理解程度。例如三角形拼成平行四边形,求得三角形面积公式是底×高÷2。此公式是否正确及具有普遍性,教学时应引导学生自己实验,试求钝角三角形、直角三角形的面积公式。
然而问题的解决大量表现在新知识的应用过程,新知识的应用主要是做练习。为评价学生知识应用的正确性及熟练程度,引导学生自编习题不失为一个好策略。在实践中发现,叙述编题是按“模仿—变式—创新”的过程而进行的。无论哪一级水平的学生,自编习题并解答,对条件信息和问题信息关系的理解都比教师提供的习题要深刻得多。实践发现学生编题时,思维呈扇形式开放状态,以学生练习中易混易错的较多。编题过程是按一定的方法对知识重新编码和组合的过程。,因而也是一种创新性的学习活动。可大大提高学生自我评价能力。
以上几方面的策略,在实际教学中是密切联系的、交叉结合的,但不管哪方面的学习策略,都必须让学生主动参与教学活动的全过程,才能真正转化成有使用意义的学习策略。