首页 -> 2007年第6期
数学问题解决与创造力发展的实证研究
作者:尹玉枝 夏子厚
一、实验假设
本实验的实验假说是数学问题解决教学有助于培养学生的创造能力。
二、研究方法
1.被试者
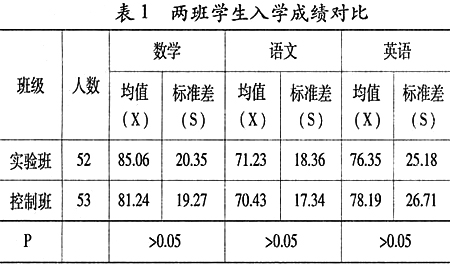
本次实验研究的被试是我市某中学两个班级共计105名学生。被试的选取采用随机抽取现存自然班的方式完成,其中甲班为实验班,乙班为控制班。根据两班的入学成绩(表1)来看,无明显差异。我们以现行的数学教材所学的内容为实验内容。
2.自变量
实验的自变量为问题解决教学的过程中不同的教学方式,即针对同样的教学内容,对实验班和控制班采取不同的教学设计和教学方式。
3.因变量
实验的因变量是学生的创造能力,这是因变量的抽象定义,而因变量的操作定义则是指用以具体衡量学生创造能力的各项指标,例如思维的广度、思维的深度、思维的灵活性、思维的发散性、思维的批判性及综合概括、归纳类比等多方面的能力。
4.实验因子
根据研究假设,我们设计了如下的实验因子:(1)在课堂教学中尽可能地以实际问题引入课题,将数学问题还原到其应有的实际背景中去,努力向学生展现将实际问题数学化的过程,指导和训练学生创设问题空间,培养学生的数学建模能力。(2)在课堂教学中以引导解决为主,综合运用其他多种教学方式。(3)在教学过程中采取多种方式,设计各种各样的变式,对学生进行多角度、全方位训练,培养学生发散思维能力,其理论基础是吉尔福特有关发散性认知加工方式的论述。(4)在日常教学中建立有效的反馈机制,对解题过程和教学内容及时进行反馈和总结,以促进学生反省认知水平的提高,其理论基础是认知心理学中有关反省认知研究成果。(5)在日常教学和课外学习中开展小组学习等集体学习的方式。(6)开设数学活动课。
5.研究程序
本实验采取了不等组前后测设计。在实验开始前先进行了创造力前测试,以确定实验组和控制组的创造力是否存在差异,并比较了两班学生的数学学业成绩和智商水平,实验开始后,实验组教学加入实验因子,控制组采用常规教学,在实验进行一年后,对实验组和控制组进行创造力后测验。
6.数据分析
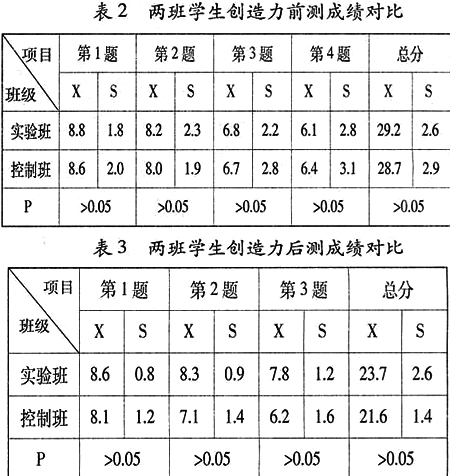
在创造力前测中,经Z—检验,二者没有显著差异(表2);在创造力后测中,二者有显著差异(表3)。
三、研究结论与启示
由上述对实验结果的分析可见,教学实验所取得的效果是显著的,实验中所设置的实验因子对于提高学生的创造能力确实起到明显的促进作用。同时,经过近一年的教学实验,实验班还在很多方面出现了令人欣喜的变化。
1.学生学习数学的兴趣空前高涨,学习成绩显著提高
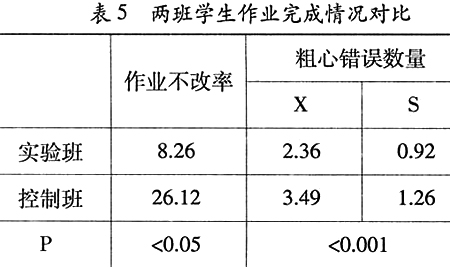
经过一年的教学实验,学生出现的最为显著的变化之一就是学习数学的兴趣空前高涨,学生们对数学课倾注了极大的热情,课上讨论积极、发言踊跃,与任课教师的配合非常默契,尤其是一些平时数学成绩比较差,上课很少主动回答问题的学生也变得非常活跃,认真思考、积极发言,与平时几乎判若两人。每周一次的数学活动课更成为学生们最盼望的时候,学生们认真执着的态度,积极热烈的讨论,取得成功后的欣喜都令我们非常感动,直到下课铃声响过很久,学生们仍久久不愿离去。学生的学习成绩有了显著提高(表4)。

2.学生的反省认知水平有所提高
经过一年的总结与反馈训练,学生的反省认知水平有所提高,逐渐养成了良好的思维习惯,不仅思路开阔,而且随时注意对自己的设想进行反省和检验,在解题后进行总结和反思,使思路清晰化、条理化,解题中出现的不切实际的荒唐错误明显减少。
3.学生运用数学语言的能力有了很大提高
常言道,“言为心声”,学生运用数学语言的能力也从一个侧面反映了学生的思维能力。由于我们在教学实验中重视对学生语言的培养,特别是采用引导解决和开设数学活动课,给了学生更多的表达自己思想的机会,因此学生运用数学语言的能力有了很大提高,无论是书面还是口头的表达都更加清晰、准确、条理清楚,这一点在创造力后测中也有明显的体现。测试中最后一道“军官选兵”问题对于中师一年级的学生来说有相当难度的。这一难度不仅表现在思维上,也表现在表达上,通过测试表明,实验组学生的表述更加清晰、准确、有条理、明显优于控制组。
4.学生间更加团结友爱,集体凝聚力增强
由于在课堂教学特别是数学活动课中较多地使用了小组学习的方式,使学生们对集体学习的方式逐步适应,并使集体学习的优越性逐渐发挥出来,小组的各个成员相互促进、相互帮助,每个学生都有发表意见的机会,在一名同学发表自己见解时,其他学生仔细倾听并共同反思,或加以验证,或加以反驳,最后形成小组共同的意见,使小组中的每个成员都有收获和提高,并且使小组成员更加团结友爱,互相支持,不把任何人孤立于讨论圈之外,使得集体的凝聚力增强。
实践证明,教学实验基本上达到了我们的实验设想,取得了比较良好的效果。同时应该看到,创造是一项复杂的心理过程,学生创造力的培养是一项长期而艰巨的任务。如何运用数学问题解决教学的模式,培养学生数学问题解决的各种认知策略,以及这些认知策略又如何影响学生创造力心理机制的发展等问题,还有待于作进一步的理论探讨和实践研究。
参考文献
[1] 徐利治等.数学与思维.长沙:湖南教育出版社,1990.
[2] 王秋海.“数学问题”探析.数学教育学报,1996(8).
[3] 李友国.问题解决的含义、策略及其教学途径.数学教学,1992(2).
[4] 袁小明.关于中国式的问题解决教学模式.数学教育学报,1994(5).
[5] 波利亚.怎样解题.阎育苏译.北京:科学出版社,1982.
(责任编辑 刘永庆)