首页 -> 2006年第6期
数学课堂中实施“再创造”教学的策略
作者:盛晓言
一、营造和谐氛围,激发创造动机
和谐的活动氛围是实施“再创造”的重要条件,因为只有在民主、宽松的活动氛围里,学生才能保持思想的开放性,善于接纳各种思想;才能独立、大胆地发表见解,并在这个基础上自由探索和自由创造。所以,教师要想方设法让课堂气氛活跃,激发学生“再创造”动机,促进学生个性发展。如在进行“平行线的特征”的教学时,教师让学生用一张不规则的纸,折出两条平行的直线,并让他们说说想法。课堂中,教师与学生一起参加折纸活动,通过小组合作探究的学习方式,师生之间、学生之间相互交流、启发,问题得到圆满解决。然后,又让学生折出一条直线截这两条平行线,此时三线八角的基本图形跃然展现在学生面前。学生根据制作的图形进行了测量,还有的学生剪下一个角,把它贴在同名的角上,用来验证这两个角的相等关系,学生在“做中学,学中做”,在这样的活动中,学生就有可能“再创造”出平行线的特征。
二、拓展活动空间,诱发创造兴趣
新课程强调:教师应挖掘课程资源,把课堂延伸到学生的生活中,让学生动手、动口、动脑,亲身经历,有较多的广泛参与的机会,并将活动中的认识与已有的数学知识和经验,建立起实质性的、非任意性的联系,从而使学生成为发现者和创造者。如教材中有一个多边形铺地的问题,教师出示一些常见的正三角形、平行四边形、正方形和正六边形组成的图案,请学生尝试用两种或两种以上的多边形拼成没有缝隙的地砖图案。课后我组织学生去商场、酒店、图书馆等场所,尽可能地搜集各种美丽的图案,并从中寻找一些规律,设计出各种各样的地板图案。由于活动时间长,动手的机会多,再加上活动中相互合作,无须教师多讲,用正多边形铺地的知识在学生的头脑里便留下了深刻的印象。活动结果证明,走进生活,不仅有助于学生再创造兴趣的培养,还可以充分挖掘学生的创造潜能,实现数学知识的“再创造”。
三、巧设问题情境,架设创造桥梁
现实世界是数学学习的丰富源泉,教师应努力创设“现实的、有意义的、富有挑战性的”贴近学生实际的问题情境,架起数学与生活的桥梁,让学生在学习“自己的数学”中,实现数学知识的“再创造”。如在进行“相似图形”教学时,展示学生美术课上的两件临摹埃及金字塔的作品(图1是教学挂图,图2、图3是学生习作),提问学生:“你认为哪幅习作临摹得较好?为什么?”学生比较后凭借生活经验作出回答:“图2临摹得较好,很像。”“图3失真了,比例不对。”教师又问:“从数学的角度而言,图2和教学挂图是何关系?”该问引导学生从数学的角度观察生活中的图形,抓住“相似图形的定义”这个已有知识,促进学生思维,学生经过测量、求对应线段比、比较、概括等过程得出相似图形的特征,实现了知识的“再创造” 。
四、连接“数学现实”,发展创造能力
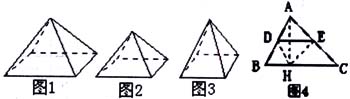
每个学生有自己的学习方式、思考方法、已有经验及相关的知识结构,即都有自己的“数学现实”。要培养学生的“再创造”,就必需以学生的数学现实为基础,找准新旧知识的联结点,引导学生“再创造”。例如,在教学“梯形中位线定理”时,教师先让学生任意画一个△ABC及它的中位线DE,让学生通过测量获得DE∥BC且DE=1/2BC的猜想。在证明这个猜想时,以小组合作的形式,通过自主探索与合作交流,学生大胆寻求新的证明途径,探究出如下添设辅助线的方法:作AH⊥BC,连结HD、HE(如图4),证得DE∥BC。
这里,教师放手让学生自己去探索,不局限书本上惟一的解题方法,而是让学生充分发表自己的意见。由于学生已有直角三角形的相关知识和垂直平分线的性质等“数学现实”,学生容易从已有经验入手,利用旧知识进行观察、分析、猜想、试验,教师再进行引导反思,让学生对自己的判断、活动、推导等过程进行思考并加以证明,用不同的方法证明了三角形的中位线问题,由于学生得到了教师尊重,潜能与个性得到了发挥和张扬,实现了知识的“再创造”。
五、精选开放习题,提升创造思维
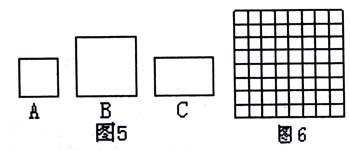
数学能力的核心是思维能力,教师必须给予广阔的思维空间。对于同一问题,要鼓励学生从不同的角度,用不同的方法加以思考,这对促进学生的“再创造”是很有必要的。在教学时,教师可结合学习内容设计一些开放性练习题,给学生一定程度的自由思考和选择的余地,这样,学生所探究的内容已不是只靠模仿和套用教师所教过的例题就可以解答,而需要创造性地应用所学知识来解决问题,学生在寻求解答过程中寻找恰当的解题策略,在实践过程中强化“再创造”的心理态势,从而对数学的本质产生新的领悟,体会到“再创造”的乐趣。如在教学中让学生解决下面的问题:现有足够的2×2,3×3的正方形和2×3的矩形图片A、B、C(如图5),现从中选取A型图片3块,B型图片1块,再选取若干块C型图片,在图6中拼成一个矩形,请你在下面给出的方格纸中按要求画出示意图(说明:下面给出的方格纸中,每个小正方形的边长均为1, 拼出的图形,要求每两个图片之间既无缝隙,也不重叠。画图必须保留拼图的痕迹)。
在学习活动中,许多学生对“选取若干块C型图片”采用凑的办法,在方格纸上对C型图片的块数逐个试验,得到答案,但很费时费力。在此情况下,有一位同学提出用数形结合的方法:设A型图片的边长为a,则面积为a2,B型图片的边长设为b,则面积为b2,可知C型图片的面积为ab,不妨先从代数恒等式3a2+xab+b2=(3a+b)(a+b)的角度找出x的值,确定C型图片的块数和矩形的边长,将原问题转化为分割问题。在此思路的引领下,全体同学分组讨论,寻找解题方法,发现此法思路简捷、操作简单,大家从中体会到了数学思想方法在解题中的重要作用。
六、尊重个体差异,促进均衡提高
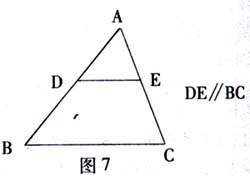
学生的数学表现存在差异是数学教学教育中的普遍现象。如何面对学生程度的差异,促进每个人在“再创造”中达到不同的水平?首先,教学中要建立多重目标,即对优等生,要求“再创造”有较高的目标;针对学困生,建立以合格为标准的“再创造”目标,让这些学困生在小组合作学习中、在活动中积极参与,有所发展。其次,教学时,要为全体学生的发展创造条件,在大纲所规定的全体条件下,允许不同水平的学生选择不同水平的数学活动,允许他们的“再创造”达到不同的程度,每个学生应充分享有“再创造”的自由。如八年级下册“探索三角形相似的条件”一节教学中,在得到“两角对应相等的两个三角形相似”的判定方法后,教师提供以下素材:如图7,D、E分别是△ABC边AB、AC上的点,DE∥BC。由以上给出的条件,你可以提出哪些问题?这些问题又如何解决?学习好的学生提出问题:图中有多少成比例的线段?这时,教师请优等生说说解决该类问题的思路,全体学生分组讨论解题的方法。有一组学生提出:若D、E分别是△ABC边AB、AC延长线上的点,DE∥BC,或D、E分别是△ABC边BA、CA延长线上的点,DE∥BC,是否还有上述结论。教师让优等生画出图形,引导全组学生展开探究,使不同水平的学生达到不同水平的“再创造”。
综上所述,在新课程视界下,实施“再创造”教学能促进学生积极参与数学实践活动,使学生从“学会”到“会学”,从而提高其创新能力和整体素质,值得我们去进一步研究和探索。
(责任编辑李海燕)