首页 -> 2006年第6期
中学物理“相对论”教材教法新思考
作者:侯建新
一、“狭义相对论”的基本原理是什么
1.相对性原理:在所有的惯性系中,物理学上的基本定律是相同的。
2.光速不变原理:在所有的惯性系中,真空中的光速具有相同的量值c。
所谓相对性原理是指所有物理学的基本规律在不同的惯性系中具有相同的形式。
所谓光速不变原理是指光的传播速度与所选择的参考系无关。在同一参考系中,光速与光传播的方向以及光源是否运动也无关,这个原理不仅指明光的传播服从相对性原理,而且指明光速c永远是个物理常数。
我们只讨论涉及无加速度的惯性系(即适用牛顿运动定律的参考系),所以叫作“狭义相对论”。应当指出,上述“狭义相对论”的两条基本原理的正确性,经受住了由它们所推导出的结果与物理事实相符合的考验。
二、何为“同时性的相对性”
爱因斯坦从十六岁开始就思考牛顿的绝对时间这个问题。经过十年的思考,他终于得出了一个异乎寻常的结论:时间的量度是相对的!也就是说,对不同的惯性系,同样的先后两个事件之间的时间间隔是不同的!对这个结论的论述是从讨论“同时性”概念开始的。在1905年那篇题为《论动体的电动力学》的著名论文中,他写道:“如果我们要描述一个质点的运动,我们就以时间的函数来给出它的坐标值。现在我们必须记住,这样的数学描述,只有在我们十分清楚懂得‘时间’在这里指的是什么之后才有物理意义。我们还应该考虑到,凡是时间在里面起作用的我们的一切判断,总是关于同时事件的判断。比如我们说,‘那列火车7点钟到达这里’,这大概是说,‘我的表的短针(时针)指到7同火车到达是同时的事件’。”
从爱因斯坦的上述论述中,我们注意到了同时性。我们还会发现,和光速不变原理紧密联系在一起的是,在某一惯性系中同时发生的两个事件在相对于此惯性系运动的另一个惯性系中观察并不是同时发生的。如图1,有两个惯性参考系,S、S′,其中S′相对于S以匀速率u向右运动。设在参考系Sv中的x′轴上的A′、B′两点各放置一个光接收器,在A′与B′的中点M′上有一闪光灯,今设光源发出一闪光,由于A′M′=B′M′,而且向各个方向的光速是一样的。所以光必将同时传播到两个光接收器,或者说,光到达A′和到达B′这两个事件在S′参考系中观察是同时发生的。

为何呢?如图3,因为光从M′出发到达A′这一段时间内,A′已迎着光线走了一段距离,而在光从M′出发到达B′,这段时间内,B′却背着光走了一段距离,显然光线从M′出发到达A′所走的距离比到达B′所走的距离要短,由于光速不变,必定是光先到达A′后到达B′,或者说,光到达A′和到达B′这两个事件在S参考系中观察并不是同时发生的。
从上面的例子中,我们发现,在光速不变的前提下,我们对“同时”概念产生了新的认识,即“同时性”是相对的,这就是“同时性的相对性”。
三、为什么钟变慢啦
在两个相对运动的惯性参考系观察先后发生的两个事件之间的时间间隔,其情况又如何呢?
如图4,在S′参考系中放置一闪光灯和光接收器于Q′处;在O′上方的M′处放置一反光镜,设O′M′=d。在S′参考系中观察,从光源O′处发光,传播到M′经反光镜反射再返回O′处,光经历的路程为2d,所用的时间为△t′=2d/c,而在S参考系中观察如图5,光源发光经过一段时间到达O′,由于O′、M′都固定在S′参考系,从S参考系中看,O′、M′都以速度u向右运动,从O′发光到M′再回到O′走的是一条折线,路程为2l=2

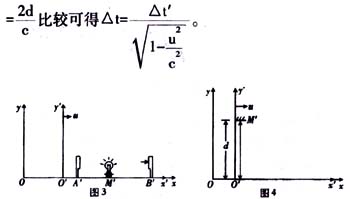
我们把S′参考系中同一地点O′先后发生的两个事件之间的时间间隔叫做固有时。显然,固有时最短,而在S系中观察到的这两个事件之间的时间间隔为固有时的
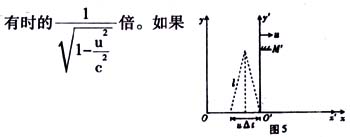 用钟表走的快慢来说明,就是S参考系中的观察者把相对于它运动的钟(即S′参考系里的钟)和自己的钟对比,就会发现那只钟变慢了,这个效应叫做运动的钟的时间延迟。
用钟表走的快慢来说明,就是S参考系中的观察者把相对于它运动的钟(即S′参考系里的钟)和自己的钟对比,就会发现那只钟变慢了,这个效应叫做运动的钟的时间延迟。
应该清楚,时间延迟只是一种相对效应,也就是说,S′参考系中的观察者会发现静止于S参考系中而相对于自己运动的钟比自己所在的参考系里的钟走得慢,此时S参考系中的一只钟给出固有时,而S′参考系中的钟给出的不是固有时。
 △t′,所以在我们日常生活的环境中是感觉不到时间的延迟效应的,只有在物体的运动速度接近光速时这种效应才十分明显。在现代高能物理中,时间的延迟效应可以从各类高速运动的粒子寿命的研究中得到证实。
△t′,所以在我们日常生活的环境中是感觉不到时间的延迟效应的,只有在物体的运动速度接近光速时这种效应才十分明显。在现代高能物理中,时间的延迟效应可以从各类高速运动的粒子寿命的研究中得到证实。
四、尺子缩短是真实的吗
我们首先应该明确,长度测量是和同时性概念密切相关的。在某一参考系中测量尺的长度,就是要测量它的两端点在同一时刻的位置之间的距离。这一点在测量静止的尺的长度时并不明显重要,但在测量运动的尺的长度时,对同时性的考虑就具有决定性的意义了。根据爱因斯坦的观点,既然同时性是相对的,那么长度的测量也必定是相对的。
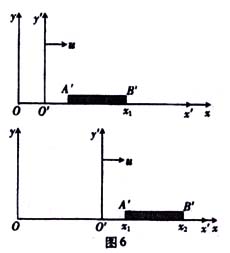
如图6,有一根尺子A′B′固定在x′轴上,在S,′参考系中测得它的长度为l′,称为固有长度。为了求出它在S参考系中的长度l′,我们设在S参考系中某一时刻t,B′端经过x1处,△t时间后,即t+△t时刻A′又经过x1处,由于尺子的运动速度为u,在t+△t这一时刻,B′端的位置一定在x1处,而x2=x1+u△t,根据长度测量的规定,在S参考系中尺子的长度应该是l=x2-x1=u△t,其中△t是在S参考系中x1处看见B′端与A′端相继通过这两个事件的时间间隔。它符合固有时的定义,所以△t是这两个事件之间的固有时。
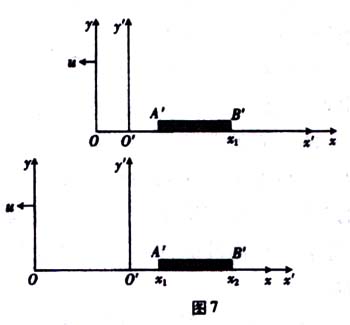
如图7,从S′参考系中看,尺子是静止的。由于S参考系向左运动,在x1这一点先通过B′点后又经过△t′,时间通过A′点,x1点的运动速率也为u,则△t′=l'/u。其中,△t和△t′分别指在S参考系和S′参考系中同样两个事件之间的

这说明一根静止的尺子长度为l′,当它相对于S参考系运动时,在S参考系中测得它的长度l要比静止时短,这种效应叫作运动的尺子长度缩短效应。也应该指出,长度缩短也是一种相对效应,静止于S参考系中沿x方向放置的尺子,在S′参考系中测量,其长度也要收缩,此时l是固有长度,而l′不是固有长度。
尺子的长度缩短效应是真实存在的,科学家对人造卫星上的尺缩效应观测发现,当卫星以8.1km/s的速度绕地球运行时,卫星上的一把米尺缩短了原来的万分之一,也正是因为这样的缩短尺寸还不到一根头发丝的直径,所以我们几乎觉察不到,更不用说我们在日常的生活环境中根本达不到8.1km/s的速度了。如果我们置身于微观的粒子世界,那情况就大不相同了,因为运动速率接近光速的粒子比比皆是,我们看到的尺缩现象也就极为普遍了。
(责任编辑孙晓雯)