首页 -> 2006年第6期
物理实验的设计与仪器选择
作者:药树栋
一、测量仪器的选择
对于直接测量,所用仪器的选择比较容易,只要使仪器的极限误差不大于被测量要求的极限误差则可。对于间接测量,误差将是各直接测量误差以某种方式的合成,从而首先应清楚误差的传递关系。设x1,x2,…,xm为直接测得量,相应的直接测量误差为△x1 >,△x2,…△xn,间接测得量用Y表示,相应的间接测量误差为△Y,它们的函数关系为Y=F(x1,x2,…,xm),在考虑误差之后则为
Y+△Y=F(x1+△x1+x2+△x2,…,xm+△xm)
按照泰勒公式展开上式并略去△x的二次方及以后各项可得

由于误差本身的正或负是不可知的,考虑到误差可能出现最大值,上式右侧各误差项均取绝对值,于是相对误差可写为
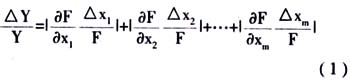
如何利用误差传递关系,在对间接测量的精确度提出了一定的要求之后确定各直接测量的精确度,从而确定直接测量所用仪器的精密度,即如何根据实验要求选择实验所用仪器,是我们必须考虑的问题。
假设间接测量值Y是由x1,x1,…,xm共m个各直接

当事先对测量提出的精确度要求为△Y/Y≤E时,如何将其分配给直接测量各项的方案有无限多个,但通常是首先考虑采用误差等分配方法,就是使
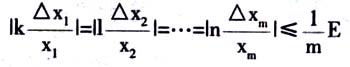
例如对x1的测量,则要求|△x1|≤1/(|k|m)Exx1,当已知x1的概值时,就可由1/(|k|m)Ex1的大小确定测量x1时应使用何等精密度的仪器。一般的原则是使所用仪器的最小分度值或仪器的感度等于或小于1/(|k|m)Exx1。
为了对该问题有更深入的了解,下面通过实例进行说明。
问题1:通过测量直径D及高h求圆柱体的体积V。设其直径和高的概值分别为D≈0.8cm,h≈3.2cm,如果要求△V/V≤1%,如何选择测量直径和高的仪器的精密度。

因为h≈3.2cm,则△h≤0.016cm=0.16mm,这样选用最小分度值为0.1mm的游标卡尺即可满足要求。而D≈0.8cm,则△D≤0.002cm=0.02mm,如果用最小分度值为0.1mm的游标卡尺已不能满足要求,这时可选用最小分度值为0.01mm的螺旋测微计去测量。看出虽然上述两个量均为长度,但却需要不同精密度的仪器去测量才能满足实验要求。
二、实验的设计
当实验要求的精确度仪器难以满足,或由于条件限制只有某种精密度的仪器时,在这种情况下如何用精密度较低的仪器达到实验精确度的要求,或如何最大限度地提高实验的精确度,就成为实验设计任务的核心。下面仍通过实例来说明。
问题2:用天平和量筒测量固体的密度,已知天平的感量是1g,量筒的最小分度为1cm3,假定所测固体的密度值约为2.6g·cm3。
理论公式为ρ=m/V2-V1,其中m为固体质量,V1、V2分别为固体放入前水的体积和固体与水的总体积。由公式(1)得

因为天平的感量为1g,量筒的最小分度值为1cm3,所以△m=0.5g,△V2=△V1=0.5cm3(实际的直接测量误差一般总是小于仪器最小分度值或感量的1/2),从而有

显然,增加固体的体积,即增加被测量的绝对值,虽然使用精密度相同的仪器测量,其相对误差△ρ/ρ将显著减小,从而提高了实验结果的精确度。
在以上的讨论中,没有考虑各直接测量误差的符号在实际上不可能全部相同,它们传递给间接测量结果时有相互抵消一些的可能性,然而我们无法判断各误差的实际符号,从最不利的情况考虑,将绝对误差或相对误差直接相加(取绝对值),这样估计的误差将有些偏大,所以实际的实验结果应小于如此估计的误差,或者说实验结果的精确度一般将高于实验设计时所要求的精确度。
参考文献
[1]杨述武.普通物理实验.北京:高等教育出版社,2001.
(责任编辑孙晓雯)