首页 -> 2006年第6期
信息技术与中小学数学教学整合例析
作者:周新莲
1.中小学数学教师样本的选取
笔者对所任教的04级本科学员展开调查,他们来自广东省各地?熏具有一定代表性。发问卷78份,收回问卷78份。统计情况表明很有必要加强信息技术教育。
2.调查内容的选取及初步调查
通过“储蓄问题”的具体实例考查学员两方面情况:一是对中小学数学新增加内容——储蓄问题的关注和掌握程度;二是用分段函数的宏观描述和微观刻画(分段函数分段点是跳跃间断点,每次结算后把所得利息并入本金自动转存的当日所处位置的点是分段函数的跳跃间断点)的水平。
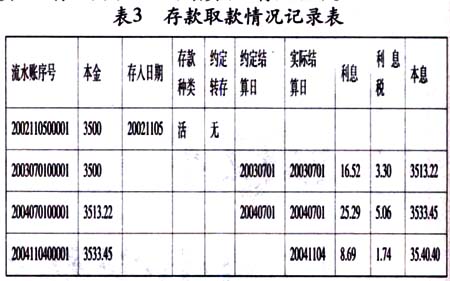
采用考试调查是因为试卷所反映的是调查对象最真实的情况,试卷回收有效率也最高。C语言中考一编程题:某人2002年11月5日在建行存活期存款人民币3500元,银行挂牌活期年利率是0.72%,计算某人今天(2004年11月4日)结算的本息(本息是本金和利息之和)。
此题考查学员活期存款结算。银行规定活期每年7月1日(中国建行、工行、农行等银行约定的结算日)结算一次,存款(元以上才计息,存款在1999年11月1日后产生的利息所得,依法纳20%个人所得税)所得利息作本金自动转存为活期,为了方便计算,把年利率转成日利率,其计算公式:
存期t=(结算年-存入年)×360+(结算月-存入月)×30+(结算日-存入年日)
利息b=本金p×年利率i360×存期t
利息税=利息b×20%
本息y=本金p+利息b×(1-20%)
试题正确的解答是结算了三次:
2003年7月1日第一次结算:
存期:t=(2003-2002)×360+(7-11)×30+(1-5)=236
y=3500+3500×0.72%360×236×(1-20%)=3513.216≈3513.22
2004年7月1日第二次结算:y=3513.22+3513×0.72%×(1-20%)≈3533.45
2004年11月4日(储户请求结算)第三次结算:
t=(2004-2004)×360+(11-7)×30+(4-1)=123
y=3533.45+3533×0.72%360×123×(1-20%)≈3540.40
统计结果归为六种:
①y=p×(1+i)t,t=2年,10人如此作答,他们知道活期利息为一年结算一次的复利算法;但存期还差一天才两年为错误一,错误二没有扣20%的税。
②y=p+p×i365×t
t=(2004-2002)×365+(11-11)×30+(4-5)
其中年利率转变为日利率,存期以天计算,3人这样作答。错误一次没有按银行规定一年按360天计算存期;另有错误活期一年内为单利算法,没扣税。
③y=p+p×i×t
t=(2004-2002)×365+(11-11)×30+(4-5)
12人这样作答。学员按天算存期。错在不知道银行规定一年为360天,仍用年利率计算:活期一年内单利计算,之后利息也计算;没有扣税。
④y=p×(1+i×t),t=2。有26人这样作答。错在活期利息为单利计算;存期计算不准确;没扣税。
⑤y=p×i×t,t=2。有1人这样作答。错在活期利息为单利计算;存期计算不准确;没有累计本金;没扣税。
⑥有26人作了与本息计算离题的作答或卷面空白,说明这些学员不具备银行储蓄方面的知识。
统计结果表明约有三分之一中小学数学教师不知道储蓄问题的解决;绝大多数中小学数学教师不知要扣利息所得20%的利息税。总之,中小学数学教师缺乏新课程内容——储蓄知识。
二、对调查内容进一步探索和实验
学员起初对笔者要求上网查阅储蓄的相关资料并不热心,按表1要求完成储蓄问题的作业,作业统计显示大部分学员只达到作业一二级的要求。

针对学生的不热心,笔者对储蓄问题的解决进行引领。查阅储蓄主题的相关资料,把中华人民共和国银行存款的10次利率变动数据用二维列表(见表2,C语言结构体数组)存放。一笔存款的结算以时间为自变量、本息为因变量绘出分段函数,但这个分段函数端点处的函数值(即对函数的微观刻画)很多学生没有准确刻画:哪怕差一天就到期,未到约定结算日的定期存款要结算是按结算日银行挂牌的活期利率来计息的,这样所得的利息比定期存款的利息要少得多。
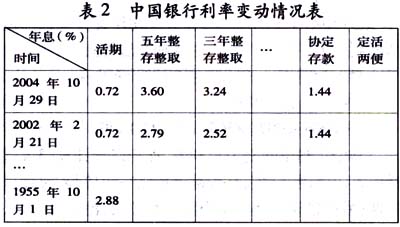
定期或活期存款的数据也是用C语言的结构体数组来存放(见表3),由于存期与约定结算时间之间有三种情况,因此储蓄问题最具本质的特征抽象和概括为函数f的三个表达式,其中结算出的本息记为f,本金p,约定结算日期t天,连续转存m次,年利率i(活期的标为i0,为结算时的年利率;定期的标为it,为存入时的年利率),存期n=(结算年-存入年)×360+(结算月-存入月)×30+(结算日-存入日)。
编程调试用存折数据来验证。把银行储蓄问题抽象概括为数学问题、解决数学问题,获得程序化、机械化的结果,本调查实验的结果只应用于活期和定期种类存款,其他尚待解决。
三、调查和实验结果的思考
面对中小学数学课程改革,通过储蓄问题的调查和实验结果的分析,思考如下:
1.高师教师在信息技术课教学中整合中小学数学课程内容,寻找出多媒体、计
算机和网络技术与学科教学自然融合的关联点对学员进行适当引领,期望课程整合活动能够培养和提高学员多方面的能力,为学员未来工作和生活做准备。因为学员在校的学习方式更能直接影响到他们毕业后的教学方式,对成人学员的影响尤为深刻。
2.目前课程改革正在我国各省市全面铺开,从调查的结果来看大部分学员(中小学教师)对课程改革理解不够,故建议高师数学教育专业开设“中小学数学课程改革”的选修课,建议这门选修课是整合数学新课程培训、练习、科研和教学实践于一体的“综合课”,“综合课”成为中小学数学课程改革顺利进行的奠基石。
3.教育不是灌输,而是点燃火焰(苏格拉底语)。对数学新课的调查和实验为职前教师和在职教师任新数学课程的教学做铺垫,主要修行还看他们今后的教学生涯。
(责任编辑李海燕)