首页 -> 2007年第8期
数学教学中可多用“比较”
作者:吴汝萍
一、 在比较中概括
数学中概念的形成、性质的理解、法则的掌握,都是经过一系列的思维活动,抽象概括的结果。恰当地运用比较,有助于学生抽象出事物的本质属性,舍弃非本质属性,提高概括的能力。
如在教学国标苏教版四年级(上册)《运算律》单元《加法交换律》时,先让学生观察情境图,明确要解决的问题是“跳绳的有多少人”后,让学生列式计算并交流算法,得到两个算式:
28+17=45(人) 17+28=45(人)
这时引导学生比较:这两个算式哪儿不同?哪儿相同?从而使学生初步感知到“两个加数交换了位置,和不变”,并用等式表示出它们之间的关系:28+17=17+28。再让学生列举出这样的等式,进行更多的验证,体验这种现象的普遍性。教师则根据学生交流的情况适时有序地把一些有代表性的等式写在黑板上:
28 + 17 = 17+ 28
10 + 20 = 20+ 10
0.4 + 0.5 = 0.5+ 0.4
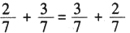
……
这时,再让学生对这些等式作进一步的观察和比较,引导学生用自己的语言归纳概括出自己发现的规律,并让学生用自己喜欢的文字、图形或字母表示出来:
甲数+乙数=乙数+甲数
△+○=○+△
x+y=y+x
……
学生经过自己的观察比较,再用自己的语言来概括、讲述加法交换律,便能实实在在地理解了加法交换律。
二、 在比较中迁移
奥苏伯尔指出,迁移现象普遍地存在于人的活动中,凡有学习的地方就会有迁移。迁移就是一种学习对另一种学习的影响。凡是一种学习对另一种学习起着促进作用与积极作用的称为正迁移;反之,一种学习对另一种学习产生干扰、起消极影响的就是负迁移。教学中,充分将新旧知识进行比较可以促进正迁移,防止负迁移。
1.新旧比较,在类比求同中促进正迁移。新旧知识的相同总是实现知识迁移的基础。一个积极的迁移过程,总是在利用相关的旧知时,认真寻找它与新知的相同要素,通过相互作用去同化或顺应新知,或将原有的认知结构包摄进来,或扩展到新的认知结构中去。
如教学国标苏教版一年级(上)“9加几”时,先出示9+1+2、9+1+5、9+1+7这样的连加,让学生比较这些连加算式有什么相同的地方?能不能很快算出得数?并说明理由。然后将这些连加算式的后两个加数合并,依次改为9+3、9+6、9+8。再让学生对照比较:
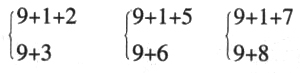
每组上下两题有什么相同的地方?上面的连加算式能用凑成10的方法很快算出得数,那下面的9+3、9+6、9+8怎样想也能很快算出得数呢?通过比较,学生就能把“凑十法”迁移到9加几中来,再通过操作,学生就能较快地掌握用“凑十法”算9加几,进而再迁移到8加几,7加几等20以内的进位加法中去。
2.新旧比较,在对比求异中防止负迁移。小学数学教材中,由于一些知识的差异性常常为它们的相似性、相近性和相关性所掩盖。有的条件相似、形式相同,表述相近而结论大相径庭,这便容易产生负迁移。通过比较,找出虽是细微却是本质的差异,可以有效地防止负迁移。如小学生初学乘法应用题时,与以往学的加法应用题相互干扰,易产生负迁移。如国标苏教版一年级(下)第89页就安排了这样一道题:
小兰说:“我家栽了2行桃数,每行6棵。”
小芳说:“我家栽了2行桃树,一行6棵,一行4棵。”
哪一家栽的桃树多?多多少棵?
先引导学生合理地组织信息,在求小兰家和小芳家各有多少棵桃树时,让学生比较算法的差异:求小兰家的桃树,是求2个6棵是多少,用乘法计算好;求小芳家的桃树,是把6棵和4棵合起来,该用加法计算。这样对比后,学生就能体会加法与乘法的联系与区别,分清加法和乘法在本质上的差异,有效地防止了负迁移。
三、 在比较中分类
一切事物只有分门别类加以研究,才能区别事物间的千差万别,明确事物间的联系。分类是以比较为基础,按照研究对象的相同点和不同点,根据一定的标准将对象区分为若干类别的一种思维方法。引导学生在比较中分类的过程是发展逻辑思维的过程。
如在给三角形按“角”分类时,先出示各种形状的一组三角形,让学生观察比较每一个三角行分别有三个什么类型的角?哪些三角形可以归为一类?为什么?进一步比较:这些三角形的三个角中有什么相同的地方?(都有两个锐角)有什么不同的地方?(另外一个角不相同,有的是锐角,有的是钝角,有的是直角)如果给这三类三角形分别起个名字,根据相同点起好,还是根据不同点起好呢?分别可以起个什么名字?教师根据学生的讨论交流情况依次板书成下表:
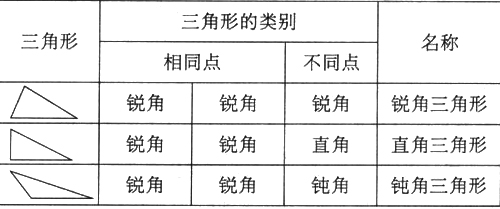
再根据比较分类的结果,引导学生为这三类三角形下定义:什么样的三角形是钝角三角形?什么样的三角形是直角三角形?能不能说有一个锐角的三角形是锐角三角形?为什么?那到底什么样的三角形才是锐角三角形呢?通过比较,学生掌握了这三类三角形的本质特征,学会了按“角”给三角形分类,体验了概念的形成过程,提高了逻辑思维的能力。
四、 在比较中建构
小学生在每一课的学习中所获得的知识常常是局部的,分散的,会有“见叶不见枝、见木不见林”的现象。通过对所学知识的纵横比较,有助于学生沟通知识间的内在联系,理清知识的来龙去脉,使知识串联成线,联结成网,建构起合理的知识结构,逐步使所学的知识系统化。
1.纵向比较连点成线。对同一层次上的不同知识进行纵向比较,利于学生将各知识连结成知识线、知识链。
如在学生分别学过长方形、正方形、平行四边形、三角形、梯形的面积后,将它们的面积公式进行比较,异中求同,逐步建构起下面的知识结构:
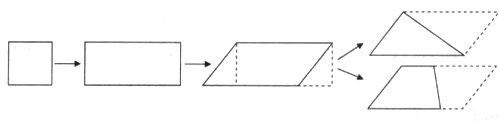
通过纵向比较,学生理解和掌握了求不同平面直线图形面积的方法,又了解了它们之间的内在联系,使思维更具条理性。
2.横向比较,连线成网。对不同层次的相关知识的内在联系进行横向比较,有助于学生头脑中的知识线、知识链构成知识网。
如在学生学过“比”后,引导学生将除法、分数、比这三个概念列表比较,找出这三者之间的相互联系和区别:

通过比较,不仅进一步深化了对这三个概念的认识,而且达到了理解知识系统化的目的。
五、 在比较中拓展
俗话说得好:“有比较才有鉴别”,“真理越辩越明”。要想让学生对一些数学知识有清晰的认识,深刻的理解,比较是最好的方法。
如苏教版二年级(上册)的“除法”单元中,在学生认识“分一分”后,在第5页上安排了“两种分法的对比”。教学时,可以先引导学生找出这两种分法的不同之处:
一是分的要求不同,左边一题是要求把12朵花,每3朵插一瓶;右边一题是要求把12朵花平均插在4个花瓶里。
二是分的方法不同,左边一题是几个几个分,结果有4个3,说明能插4瓶;右边一题是一个一个分,结果每个花瓶能插3朵。
再引导学生异中求同,找出这两种分法的相同之处:
一是分的物品相同,都是分12朵花。
二是分的结果相同,都是平均分。
通过比较,帮助学生把平均分的不同方法加以整合,让学生体会把一些物体平均分,既可以每几个一份地分,也可以平均分成几份,分的过程虽然有所差别,但分的结果都是相同的,所以都是平均分,从而在整体上使学生进一步深化理解了平均分的含义。
责任编辑:陈国庆