首页 -> 2007年第3期
匡正数学训练与发展思维的关系
作者:龚 健
一、 熟能生巧的陷阱
课堂片段回放:教学《圆锥体积的计算及应用》
1.教师在提问圆锥的体积怎样计算后随即让学生口算下列各圆锥的体积:
(1)底面积3平方米,高2分米。
(2)底面积4平方厘米,高4.5厘米。
小结:应用圆锥体积的计算公式求圆锥体积时,不能忘记乘1/3或除以3。
2.出示例2:一个圆锥形的沙堆的底面直径是6米,高1.8米。每立方米沙重1,7吨。这堆沙约重多少吨?
学生尝试解答后交流反馈。
小结:注意求圆锥体积时,一定不能忘记乘1/3或除以3。
3.组织练习
(1)练一练
求下面各圆锥的体积:
底面半径2厘米,高6厘米
底面直径2厘米,高6厘米
底面周长25,12米,高6米
(2)练习三第9题
一个圆锥形小麦堆底面周长是12.56米。高0.6米,如果每立方米小麦重745千克,这堆小麦大约多少千克?,
学生独立算后交流。
最后强调:计算圆锥体积需要知道底面积和高。如果不知道底面积,要先求出半径算出底面积,再计算体积。求体积时特别要牢记乘1/3或除以3。
无独有偶,三天后该校进行了质量调研,试卷上出现了圆锥体积计算的题目:
题目1:如果一个圆柱体和一个圆锥体等底等高,它们的体积一共是48立方厘米,那么圆锥的体积是()立方厘米。已知圆锥的底面积是9平方厘米,它的高是()厘米。
题目2:把一个底面积45平方分米、高7分米的圆柱体钢块,铸成一个圆锥体零件,这个零件的体积是()立方分米。已知这个零件的高是9分米,那么它的底面积是()平方分米。
探讨
这位老师班上的学生第1题的得分率为88%,而第2题的得分率仅为28%。这两道难度相仿的题,为什么会出现那么大的差别?在平时的练习中,这位教师注意强调了等底等高的圆柱和圆锥体积间的关系,重视了圆柱、圆锥体积公式的实际应用,所以第1题的得分率较高。但在应用圆锥体积公式求体积时,教师常常会提醒学生乘1/3或除以3。在大量的重复练习后,学生一看到求圆锥体的体积就条件反射地乘1/3或除以3,所以第2题的第1空多数学生出现了这样的错误。
《数学课程标准(实验稿)》在总体目标中明确提出,通过义务教育阶段的数学学习,学生能够获得适应未来社会生活和进一步发展所必需的重要数学知识(包括数学事实、数学活动经验)以及基本的数学思想方法和必要的数学技能;初步学会运用数学的思维方式去观察、分析现实社会,去解决日常生活中和其他学科学习中的问题增强应用数学的意识等等。上面的数学活动,看上去学生似乎在大量模仿练习中已经熟练掌握圆锥体积计算公式,但令人担心的是:少了变式训练的题目,少了发展思维的题目,少了解决现实问题的题目。在平时的数学教学中,常常会出现这样的现象:教师精细地讲解例题后,学生能很快掌握一类题的解题技能,经过一段时间的反复操练后,学生的解题技能进一步提高,但遇到稍有变化的习题或具体的问题情境时,学生或变得不愿思考,机械照搬;或不会思考,一筹莫展。学生在一味的机械训练中究竟学到了什么?是数学思维还是应用意识?
二、“最优化”一定“最优”吗?
课堂片段回放:教学《长方形、正方形的周长》
在巩固练习环节老师出了这样一道题:
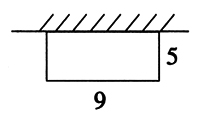
王大伯借助一面墙用篱笆围一块长方形菜地(如图)求篱笆的长度。
反馈校正时学生出现了这样4种解题方法:(9+5)×2 (9+5)×2-9 9+5×2 9+5+5
探讨
第一种显然是错误的。第2、3、4种方法中,少数学生用了后两种方法,根据平面图形周长的意义,直接把三条边相加,多数学生是先套用周长公式求出长方形的周长,然后再减去一条长,求出篱笆的长度,出现这样的结果,可能是教师在学生尚未充分理解周长的意义和计算方法的情况下,过于强调用长方形周长计算公式解题,导致学生忽略周长的意义,忽视了四条边相加求长方形周长的方法。事实上,理解周长的意义是本质的,应在此基础上优化求长方形周长的算法。因此在教学中,教师要先突出最简单、最本质的方法,逐步抽象出最佳方法,进而促使学生达到认识上的最佳状态。这种过于追求解题方法的“最优化”,限制了学生的探索能力。封闭了学生的思维空间。
三、 都是“模式化”惹的祸!
课堂片段回放:教学《按比例分配应用题》
教师在教学完《按比例分配应用题》的例题后小结:告诉我们两个数量的比及它们的和,要求这两个量,可以用和分别乘总份数分之一个数量的份数,分别求出这两个数量。
当天的《练习册》出现了这样两道题:
1.一种盐水,盐和水的比是1∶99,要配置400克这样的盐水,需要盐多少克?
2.一种盐水,盐和水的比是1∶99。要配置这样的盐水,400克水中需要放入盐多少克?
这班学生作业的正确率可想而知,尤其是第2题,除了班中几位脑瓜特别好使的学生外,无人能答对。
探讨
按比例分配应用题有其特有的数量特征,教师常常会总结解题规律并进行类似练习。学生习惯于把问题和类型相联系,死扣类型,而不去思考这些问题的实际意义。于是解第2题时生搬硬套,出现不应有的错误。因此,教学中应着重引导学生把问题和其实际意义相联系,避免解题模式的“类型化”,以真正发展学生的数学思维能力。
由此可见,教学中不能把握数学过程和数学对象之间的平衡,盲目、过度的练习会影响学生理解力和创造力的发展。那么,如何匡正数学训练与发展思维的关系?笔者认为:
1.科学设计练习,剖析题目中的思想方法
科学的、一定数量的数学练习能促进理解,发展数学思维。反之,单一、重复的机械性训练也会影响学生的思考力。如果教师只依靠模仿性练习让学生“记住”知识,而非推进认知结构,就会将数学肢解成零散的小步骤来训练,活生生的数学思想就会被完全割裂,不复存在。数学训练的第一层是“知识堆积”与“解题术”式的。它看得见,摸得着,易操作,易复制,但功能性弱,应用面窄。第二层是“思维方法”和“解题方法”式的。它与前一层比,程序性弱,不易复制,但功能性强,应用面宽。第三层是“数学思想”与“数学观念”式的。它虽抽象,程序性更弱,但功能性强,它是对其他两个层次的指导和引领。所以,教师在教学中要科学地、有层次地设计练习。首先是模仿训练,旨在巩固基础知识和基本技能;其次是变式训练,旨在理解方法和发展思维;最后是应用训练。这样才能高屋建瓴,有效训练,发展学生的思维。
2.引导自主探索,理解题目中的思想方法
数学家华罗庚教授总结他的学习经历时指出:对书本的某些原理、定律、公式问题,我们在学习的时候,不仅应该记住它的结论,懂得它的道理,而且还应该设想一下人家是怎么想出来的,经过多少曲折,攻破多少难关,才得出这个结论的。只有经历这样的探索过程,数学的思想和方法才能积淀、凝聚在这些数学结论上,从而使知识具有更大的智慧,所以,在对学生进行数学解题训练时,教师要引导学生经历数学化的学习过程,巧妙地将模型化、化归等数学思想有意识地渗透在解题过程之中,这样才能促进理解,发展思维。
3.重视解题反思,领悟题目中的思想方法
在解题训练中引导学生获得数学思想方法,一方面要求教师有意识地渗透和训练,但是更多的是要靠学生自身在反思过程中领悟。在数学学习过程中,要引导学生自觉地检查自己的思维活动,反思自己是怎样发现和解决问题的,应用了哪些基本的思考方法、技能和技巧,走过哪些弯路,有哪些容易发生(或发生过)的错误,原因何在,该记住哪些经验教训等。还要让学生掌握更多的思维机制,例如内化、压缩,等等。只有这样,才能对数学思想方法有所认识,由此更好地促进学生的思维发展。
责任编辑:陈国庆