首页 -> 2005年第11期
数学教学的“启—放—收”导学策略
作者:陈 力
一、 “启发到位”是前提
听课中常有这种现象:不少教师在让学生开展独立探究或合作交流之前,由于没有讲清楚要求,或者缺少必要的“操作模式”指引,学生特别是一年级学生在开展主动学习时无从下手、“无所事事”或者杂乱无章,学习效果很差。笔者认为,学生的“动”是以教师的“启”为前提的,教师在学生主动学习之前作适当的引导,能够为学生的学习活动指引方向,扫清障碍,避免“瞎子过河”。
1.提供“自学提纲”启发学生“独立思考”
学生主动学习的第一步是独立学习,但独立学习不是简单的“自由学习”,而应该是教师引导下的有效独立思考的过程。为了使独立学习富有成效,教师应提供一个基于问题思考的“自学提纲”,为学生指引学习思路。例如,学习《有关8的计算》(新世纪版教材第一册),教师出示情景图“跳绳”,设计以下几个问题引导学生独立学习:(1)图中在干什么?(一群小朋友在操场上跳绳)(2)从图中你能发现哪些数量信息?(4个男生和4个女生,1个戴帽子的和7个没戴帽子的,3个穿裙子的和5个穿裤子的,2个挥绳子的和6个跳绳子的……)(3)你能提出什么数学问题?(如“一共有几个小朋友在跳绳?”等等)(4)你能用几种方法来解决这个问题?请列出相应的加法和减法算式。(1+7,8-7,2+6,8-2,3+5,8-5,4+4,8-4,等等)并不要求每个学生都能列出全部算式,目的是让学生经过自己初步的独立探索,为下一步开展合作交流和进一步的合作探究奠定基础。
2.提供“合作指南”启发学生“合作探究”
为了使学生的合作学习井然有序,使合作小组里“人人有事做,事事有人做”,避免“形合而实不合”或“合而不作”的现象,教师在学生合理分组的前提下,要在开展合作探究前给学生提供一个“合作指南”,使他们有一个“操作程序”。例如,学习《圆的周长》时,可提供以下一些操作步骤:(1)小组讨论:怎样根据提供的材料(圆片、细绳、直尺等)测量出这些圆片的周长?由组长主持,人人都要发言;(2)合作动手:根据讨论出来的方法,互相配合把圆片的周长测量出来;(3)再次讨论:①用这些测量方法能测量所有圆的周长吗?②能不能像正方形周长那样用公式来计算?③圆的周长可能和圆的什么有关系?(4)再次动手:通过测量和计算,探索出圆的周长和圆的什么之间存在着什么样的规律?
3.提供“交流建议”启发学生“数学表达”
当学生经过自己的独立思考后,教师要引导他们进行小组或组际之间的交流活动,让他们把自己的学习成果用数学语言表达出来。有些教师对学生的交流内容和方式不作任何引导,任由他们“自由说”,结果不少中下学生,要么在小组里“哑口无言”只做“陪伴郎”,要么就说得支支吾吾,零散无序,既浪费时间又使学生养成不良的表达习惯。因此,教师在学生交流之前应该提出一个“交流建议”,使学生“有话可说”、“有话能说”。例如,学习《统计》(国标教材第四册),出示:
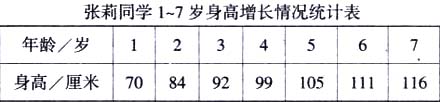
在学生独立观察和思考的基础上,组织学生进行4人小组的交流。教师提出建议:由组长安排“说”的次序,人人都要发言(不善于发言的大家要进行帮助和激励),没轮到时认真倾听(通过倾听去评价别人、反思自己),发言时围绕以下一些问题来展开:(1)从表中可以看出张莉同学的身高和年龄有什么关系?(2)哪一年龄段长得最快?哪一年龄段长得最慢?(3)预测一下,张莉8岁时可能有多高?(4)你还能提出哪些数学问题?
二、 “放得真心”是关键
1.学生能“动手”的要放手让他们去“操作”
著名心理学家皮亚杰说:“儿童的思维是从动作开始的,切断动作与思维的联系,思维就得不到发展。”因此,教师要根据所学内容的特点,凡是学生能够“动手”的地方,要放手让他们去“操作”,借助操作启动思维。例如,学习《有余数除法》,让学生进行“把7颗豆子平均分到3个盘子里”的操作。通过操作,学生明白了那个剩下来不够再分的豆子数就是“余数”,并且“余数一定要比除数小”,否则每个盘子里至少还可以再分到一颗豆子,往盘子里试着放豆子的过程就是“试商”。接着,在学生用实物操作的基础上,让学生脱离实物在脑子里分豆子。最后,让学生进行算式运算:7÷3=2…1。整个过程就是布鲁纳提出的“三个操作”的认知理论:实物操作→表象操作→符号操作。
2.学生能“发现”的要放手让他们去“探究”
教学中如果没有对问题的探究,就不可能有学生积极主动的参与,不可能有学生的独立思考与相互之间的思维启迪,也就不可能有真正意义上的主动学习。因此,教师要为学生提供探究的时空,放手让他们自己去感知和理解知识产生和发展的过程,提出独到的见解、设想与做法,完成富有个人特色的探究性作业。如:(1)可以给学生提供大量的具体事例,放手让他们去“观察——归纳”,在归纳探究过程中培养学生对问题的抽象概括能力;(2)可以给学生提供丰富的动手材料,放手让他们去“操作——感悟”,通过操作性探究,获得亲身体验;(3)可以为学生创设“实验”的情境,放手让他们去“试验——发现”,通过亲自尝试、筛选,发现规律,得出结论;(4)可以鼓励学生根据已有的知识、经验和方法,对数学问题进行大胆假设,放手让他们进行“猜想——验证”的探究活动,等等。
3.学生能“体验”的要放手让他们去“经历”
学生主体性的发展是以活动为中介的,学生只有投身于各种数学活动之中,靠自己去“悟”、去“做”、去“经历”、去“体验”,数学的知识、思想和方法才能在现实的活动中理解和发展。因此,教师要充分重视“过程教学”,要给学生提供足够的时间和空间,放手让他们去“经历过程”,不能为了“赶”教学进度而去“催”学生、“缩”过程,从而造成学生思维的跳跃。例如,教学《秒的认识》,让学生经历“看”秒针的走动,“听”秒针的声音,随秒针走动的频率“数数”、“拍手”等过程体验“1秒”的实际意义。然后,再同时观察分针和秒针,体验分与秒的关系(1分=60秒)。最后,通过多种形式的活动(做“眼保健操”、跳绳、拍皮球、做口算题等),让学生脱离钟面的辅助作用进行再体验,进而形成估测能力,使学生体验到数学的价值,体验到成功的快乐。
4.学生能“实践”的要放手让他们去“践行”
《数学课程标准》中指出:体会数学与自然及人类社会的密切联系,了解数学的价值,增进对数学的理解和学好数学的信心。而“实践”恰好是架设数学与自然及人类社会的一座桥梁,教师要当好这座桥梁的“设计师”,放手让学生运用数学的观点和方法来认识周围的事物,并能解决一些简单的实际问题。例如,当学生认识了“三角形和平行四边形的特征”后,可以在教学中展现一把摇动的椅子,让学生讨论怎样应用三角形稳定性的特征来修理这把椅子,并亲自动手把它修好。还可以带领学生到马路旁或商店内观察:哪些地方运用到三角形的稳定性?哪些地方运用到平行四边形的不稳定性?经过这种实地的观察、触摸,这些特征对学生将是终身难忘的,更为重要的是学生对生活中多姿多彩的现象有了一个本质的认识。
[2]