首页 -> 2008年第4期
数学课堂认知偏差处理的两个片段与反思
作者:朱 诚 贺璐璐
任何认知活动都可能产生认知偏差。就数学课堂这个特定环境而言,在师生对话中产生的认知偏差主要有两种:一是学生在学习中错误地理解了定义、概念、定理等,从而与正确的认识产生了偏差;另一种是学生在学习中自发形成了一种对概念或定理的正确认知,认知本身没有科学性错误,但这种认知所涉及的基本知识和方法等偏离了这节课正在进行的教学的主题,严格地说,这种认知偏差实际上只是认知偏离。
下面举一些真实教学片段加以说明。
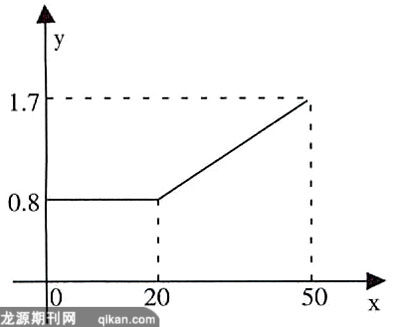
片段1:在利用一次函数图象解决问题这一节课中,教师打出这样一道题目:邮局规定平信重量不能超过20克,如果重量超出20克需要额外收取费用,所收的邮资与信件重量关系如图所示。如果有人需要邮寄35克的信件,他要付多少钱的邮资?有学生这样回答:“我觉得从20克到50克增加30克,而费用增加0.9元,那么每增加一克就要多付0.03元,所以35克的信件总共付0.8+0.03×(35—20)=1.25元。”教师听完以后未加评论就请他坐下,接着问有没有其他方法(注:本节课教师拟定的教学主题是先列方程组求出一次函数解析式后再代值计算),有学生回答说先设函数解析式为y=kx+b,由图象得方程组再解出k和b即可。教师对此大加赞许并展示事先编辑好的具体书写过程作示范。
片段2:在北师大版教材《我变胖了》一节的课堂教学中,学完圆柱体的锻压后,教师给出这样一题:将底面直径为6、高为13的圆柱形杯A中的水倒入另一底面直径为5、高为18的圆柱形杯B中,问:若杯B能装下,此时水面离杯口有多少距离?若装不下,当杯B装满水时,杯A中水面高度比原先下降了多少?有一个学生可能从两圆柱的高度差凭直觉判断能装得下,也可能是忘记判断了,他直接设水面离杯口距离是x,由题意列出方程π(3)2×13=π(2.5)2×(18-x),但在老师巡视时他还没来得及解就被教师看见了,教师立即友善地提醒他这样做是错的。
二、分析:教师所持有的教学观
看完这两个教学片段,相信不少教师都会感慨自己也曾经有过类似的经历。片段中教师的教学行为,反映出他们对教学设计与师生对话中认知偏差的处理有这样的理解:(1)客观上,教学设计先于课堂教学。这在一定程度上影响着教师形成这样的教学观:教学过程是教师帮助学生按照教学设计所预期的方向发展的过程,教师的帮助体现在尽可能高效率地促成这种发展。(2)如果教师能把事先准备好的想法(尤其是问题的解法)全部在课堂上得到贯彻,则可以认为教学过程是完整圆满的。(3)教案是课堂教学围绕的中心,具有不可更改性(除了因时间原因而进行缩减调整)。(4)教材和教师用书具有绝对的权威性:教材规定了教学设计的内容,而教师用书基本规定了教学设计的方法与模式。教学设计应较好地体现教材中的所有内容。(5)按部就班的教学设计及其实施为教师带来了便利,在一定程度上节约了教学时间,提高了教学效率。
三、反思:有没有更好的处理方式?
在这两个片段中我们可以看出,教师只关注了与自己的观点一致的学生,而忽视抱有其他不同想法的学生,这显然挫伤了这部分学生学习的主动性。只有合乎“规范”的解法才能得到老师肯定,没有十成把握就不要举手发言以免耽误老师的时间而受责怪。
1.以“谁”为中心——教案还是学生?
教案显然是实施教学时必不可少的重要组成部分。我们也应该认识到,无论教师课前多么充分地准备,都无法罗列所有学生可能有的想法。课堂上的师生对话,应从学生的口中说出答案而不是由教师来讲,这既能让教师了解学生头脑内部的反应,又促进了师生间的互动。因此,教师应该不断地作出有意识的努力,按学生自己的观点去观察他们的行为。比如在片段1中,当学生还没有学过解二元一次方程组时,有的学生想要以自己对一次函数的理解(成比例地增加或减少)来解决问题,这是合理的学习需要,即使出乎教师的意料,或者不合乎简洁的形式化标准。也应受到教师重视,而不是不假思索就置之不理。如果教师发现学生的解法比自己备课纸上的解法更好(比如使用了更少的数学知识与技巧解决问题,或者解法新颖有独创性),那么作为理性的教师应该适时调整甚至放弃原先的计划,而不是硬要把学生不感兴趣、不关心的想法灌输下去,以为这样的教学才圆满——实际上这可能是在浪费时间。总之,教师在课堂教学中过分依赖教案及事先拟定的教学程序的教学行为实质上是以教案为主体、以知识灌输为主导,很难形成师生双向互动。
2.如何找出口?——否定错误。还是把错误引入更深的思考?
如果学生给出的回答不完全正确甚至是错误的,那么教师又应如何处理呢?在片段2中,教师通常会以间接提示或更直接的方式根据已有的答案纠正学生存在的错误。可是,这样做是否对学生的帮助最大?有没有其他更好的方式?
可以肯定,即使学生回答错误,也至少表明他的思维在活动。客观地反映了学生目前的认知状况。应当承认,任何人认识新事物总是渐进的,从非本质的表象逐步深入到本质的核心,而在这个过程中难免犯错。教师在处理学生的错误时,通常会站在正确答案这一边来纠正错误,而很少会站在犯了错的学生这一边来纠正错误。在片段2中,如果教师把自己置于学生的处境中,他可能会有新发现:π(3)2×13=π(2.5)2×(18-x)的解是-0.72。这时可以引导学生进行更深层次的思考:这个解怎么会出现的?合理吗?有意义吗?你能解释它的现实意义吗?事实上,某个问题的错误答案很可能预示着另一个问题的正确答案。这个看似不正确的方程很巧妙地解决了“能否装下”的问题,只是学生尚不能认识到其中的“出口”,需要教师引导和帮助。
之所以强调对看似错误的回答进行挖掘,是基于下面的考虑:(1)保护信心与兴趣。教师对学生的评价直接影响学生学习的情绪和状态,因此有必要充分琢磨学生的回答,挖掘其中合理的部分,提出改进的建议,不轻易否定学生的想法,促进他们的深层次思考。(2)培养反思意识:在片段2中,如果教师先不动声色地让学生去解那个方程,那么学生在求得负数解后显然不得不思考这些问题:怎么会是个负数?哪里出了问题?是不是计算有误?列式不对吗?这时,教师再适时介入提供一些帮助,让全班学生参与问题讨论。这样做既让这位学生感觉到自己与教师形成双边互动,又促进他对自己解答过程的反思与监控,同时还联系了刚学过的负数,深化对负数意义的理解。