首页 -> 2007年第3期
编辑出版工作充满着数学
作者:倪 明
我学的是数学专业,主要做的是数学图书。虽然在数学上没有成就,但喜欢数学,习惯用数学方法思考问题。
不久前,因赶着出书,下厂处理稿件。在处理过程中,需添加文字,并对文字的字号、字体、位置给予明确的标注。要标注新添加标题文字的字号,先要知道原有标题的字号。有一级标题,凭经验看像是四号字,又好像是小三号,难以确定。怎么办呢?我知道1磅近似于0.35毫米,小四号字是12磅,四号字是14磅,小三号字是15磅……于是,用尺量了这级标题3个字的宽度,接近15毫米。这样可以计算得到1个字的宽度(磅),因为是近似值,可以认为是14磅,也就是四号字,问题得到解决。
这是一个用数学的简单例子,只涉及四则运算,属于小学数学,每一个编辑应当都会。问题的关键是,有没有想到用自己会的数学知识来解决遇到的问题。
其实,在编辑出版工作中,遇到数学的地方还真不少呢。下面这几个例子,可作佐证。
第一个例子是为一套书做盒子。我策划过一套数学奥林匹克小丛书,共有30种,并要为这套书做一个盒子。这样规模的书,在正常情况下,从第一本出版到最后一本出齐大约会超过一个月。如果用做封面的办法估计书脊的厚度来测算盒子的宽度,很可能估计不准。因为在估计书脊厚度时,可能会有一点误差,比如有0.5毫米的误差。这点小小的误差对一本书来说不算什么,但对30本书而言,误差的最大范围是乘法的结果,那就相当大了。如果盒子做小了,书放不下;反之,盒子做大了,松松垮垮,既不美观,又给运输带来不便,容易把图书及盒子损坏。为此,应该尽可能准确地估计这30本书的厚度。用什么办法呢?在差不多出版了一半图书的时候,办法想出来了。这时我已经知道这套书中每一册的印张数和全套书的总印张数,于是我就找来已出版的总印张数与这套书总印张数完全相等的另外30册书。所找的30册书与这套书的封面张数、内封张数、插页张数、内芯张数、用纸克重完全一致,量出所找30册书的厚度就可以确定盒子的厚度了。事实上,所做盒子的宽度恰到好处。当这套书最后一本出版的时候,盒子也刚好做完,节约了等做盒子的时间。
第二个例子是确定书号的校验码。从今年起,标准书号改用13位。以前书号是10位,其中前面9位是具有一定意义的编码,最后一位是校验码。
有一个双休日,印刷厂在即将印刷的时候,发现我们的一本书中版权页与封底上书号的校验码不一致。不一致,说明至少有一个是错的。有人问了我们的项目编辑,他回答,可参考紧邻的上一个书号。这个编辑在工作中发现不少书号的校验码比上一个书号的校验码恰好小2。如本社某本图书书号的第三段为4170,校验码为7,而和它紧邻的书号第三段为4171的图书,其校验码恰好比上一个书号的校验码小2为5。项目编辑把这件事情告诉我,我回答,让我算一下再答复这种巧合到底是不是规律。
我知道校验码有一个公式,但记忆有点模糊。我找了本社的几本图书,用依稀记得的公式尝试计算,发现不对。后来,作了一点调整,几个书号检验下来都对。我相信,修改后的方案是对的,但不是同事提供的“规律”。现在,回首这件事,能惊出一身汗,好险啊!
为了保险起见,我在网上搜索了有关书号的规定,查到了书号校验码的计算方法,结果让我很吃惊——与我给出的方案竟然不一样!这两个方案是不是等价的?当我将两种方案用公式表示出来的时候,一个新的发现又产生了:两者是等价的,只是制定校验码的人所表述的规则比我的要复杂。
国家标准《中国标准书号》的附录B介绍了ISBN校验码的计算方法。它以ISBN 7-100-01777-7为例,给出具体计算的一个表格(表1)。
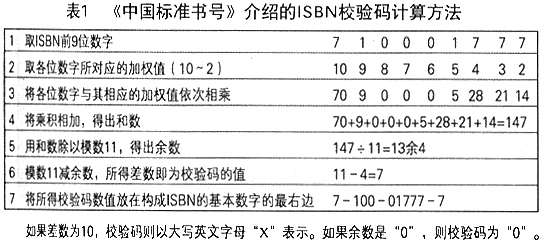
我的方案也以ISBN 7-100-01777-7为例加以说明(表2)。

两者相比较,有以下几点不同:
(1)第二步的加权值用“1~9”比“10~2”方便、好记。
(2)总共7个步骤变成了6步,且在第5步求得余数后不必求差数。
(3)“标准”中有两个特殊情形需要分别说明,一个是差数为10,一个是余数为0,较为复杂。我的方案几乎不必特别说明,当余数出现10时,用阿拉伯数字表示是2个数码,改用罗马数字“X”就是1个数码。这样保证了校验码是1位数码,书号统一为10个数码。
这个方案虽然已经没有用了,2007年起有了新的方案,但我想说的是,编辑出版工作充满着数学,用数学的方法解决编辑出版工作中遇到的问题是有趣而有效的。
第三个例子是发行折扣的确定。现在,合作出版的项目在增多。合作者往往会提出付给出版社一定比例的管理费。如果这样简单行事,也就是编辑、印刷、发行全由合作方完成,那是违背出版管理规定的。为了使这样的项目符合出版管理规定,编辑、排版、印刷要由出版社来承担,向作者支付稿酬,与合作方用批发的方式进行合作。由于印制成本与图书销售过程中均会产生增值税,而且增值税的税率也不同,因此,约定的管理费并不是销售折扣与各项成本百分比的代数和,而是要通过稍微细致的计算才能得到。假设双方商定出版社的收益是码洋的10%,排印成本为22%,稿费为6%,那么发行折扣不能用38%。可以粗略地这样计算:设发行折扣为x,因为图书销售的增值税税率是13%,排印成本的增值税税率是17%,所以
x-22%-6%-(x×13%÷113%-22%×17%÷117%)=10%,
解得x≈39.3%。这是一个一元一次方程,解这个方程并不困难。
上述的几个例子说明,编辑出版工作中充满着数学问题。第一个例子,数学使我们有效地提高了工作的效率,有利于控制出书的节奏,以把握最合适的销售时机;第二个例子,数学为我们避免了差错;第三个例子,数学为我们提供了决策的依据。其实,编辑出版工作中的数学问题还有许多。例如,标准型号纸张尺寸的自相似性,一定字号、行距下字数的计算,稿酬支付不同方式平衡点的计算,图书目标利润下运作的策略,等等。在编辑出版工作中,如果我们懂一点计算,应当是有利无弊的。因此,编辑应当尽量拓宽知识面,包括掌握有关数学知识并有意识地运用到编辑出版工作实践中,这无疑会提高我们的工作效率和工作质量。
(作者单位:华东师范大学出版社)
(责任编辑:鲍莉炜)