|
在这一章,我将只讨论事件的概率以及它引起的问题。这些问题的产生同博奕论和物理学的概率定律有关。我将什么可称之为假说的概率问题——例如一个经常受到检验的假说是否比一个很少受到检验的假说更可几等问题——留到第79至85节在“验证”题目下进行讨论。
与概率论有关的观念在现代物理学中起着决定性的作用。然而我们仍然缺乏一个满意的、前后一致的概率定义;也就是说,我们仍然缺乏一个满意的概率计算的公理系统。概率和经验之间的关系也仍然需要澄清。在研究这个问题时,我们将发现对我的方法论观点几乎不能克服的反对意见最初是什么。因为虽然概率陈述在经验科学中起着如此重要的作用,可是结果它们却在原则上不受严格证伪的影响。然而,这块绊脚石将成为检验我的理论,以便查明它有什么价值的试金石。
因此我们面临两项任务。第一项任务是为概率计算提供新的基础。我将试图通过把概率论发展为频率理论做到这一点,沿着Richard
von Mises所遵循的路线,但不用他称之为的“收敛公理”(或“极限公理”),而使用有点削弱了的“随机公理”。第二项任务是阐明概率和经验之间的关系。这是指解决我所说的概率陈述的可判定性问题。
我希望这些研究将有助于减轻目前的不满意的情况,物理学家在这种情况下大量使用概率,而未能前后一致地说明他们所说的“概率”是什么。
47.概率陈述的解释问题
我将从区别两类概率陈述开始:相数字表示某一概率的陈述——我称之为数值概率陈述——以及不用数字表示的概率陈述。
例如,“用两颗骰子掷11的概率为1/18”,这种陈述就是数值概率陈述一个例子。非数值概率陈述可以有各种各样。“把水和酒精混合获得均匀的混合物是十分可几的”,这类陈述如得到适当阐明,就能转变为数值概率陈述(例如,“获得……的概率很接近1”)。另一种很不同的数值概率陈述例如“发现一种与量子论相矛盾的物理效应是高度不可几的”;我认为这种陈述不可能转变为数值概率陈述,或者与某种数值概率陈述等价,而不歪曲它的意义。我将首先讨论数值概率陈述;非数值概率陈述,我认为不那么重要,容后再考虑。
与每一个数值概率陈述有联系的是这样一个问题:“我们应如何解释这类陈述,特别是这类陈述所作出的数值方面的断言?”
48.主观解释和客观解释
古典的(Laplace的)概率理论把某一概率的数值定义为用同样可能的情况数除有利的情况数所得的商。我们可以不理会已经提出来的反对这个定义的逻辑上的异议,如“同样可能的”不过是“同样可几的”另一种说法。但是甚至在那时我们也很难承认这个定义提供了一个可毫不含糊地应用的解释。因为其中隐含着若干种不同的解释,我要把这些解释分为主观的和客观的两类。
概率论的主观解释常常使用的带有心理学味道的说法,如“数学期望”,或者比方说,“误差的正态定律”等等,使人想起概率论的主观解释;其最初的形式是心理学主义的。它把概率的大小看作为确定或不确定、相信或怀疑的感觉的量度,这些感觉可由某些断言或推测在我们心中引起。关于某些非数值陈述,“可几的”一词可用这种方法颇为满意地加以转译;但是我认为沿着这些路线对数值概率陈述所作的阐释是十分不能令人满意的。
然而,主观解释的较新变种应该在这里给予更认真的考虑。还不是在心理学上,而是在逻辑上把概率陈述解释为关于可称之为陈述“逻辑近似”的断言。正如我们全都知道的那样,陈述能互相处于各种逻辑关系中,如可推演性、不相容性或相互依赖性;而逻辑-主观理论(Keynes是它的主要阐述者)把概率关系看作是两个陈述之间的特种逻辑关系。这种概率关系的两个极端情况是可推演性和矛盾:有人说,如陈述p从陈述q推导出,则q把概率1“给予”p。如p和q相互矛盾,则q给p的概率为0。在这两个极端之间有其他概率关系,大概可以下列方法解释:陈述声(给定q)的数值概率越大,则它的内容超出陈述q已包含的内容越少,p的概率依赖q(并且q把某种概率“给予”p)。
从Keynes把概念定义为“理性信仰程度”这一事实可看出这个理论与心理学主义理论之间的密切关系。他的“理性信仰程度”是指信赖量,可以根据我们从”给予”陈述p概率的那个陈述q中得到的信息或知识赋予p以信任量。
第三种解释,客观解释,把每一个数值概率陈述看作为一种相对频率的陈述,某一种类事件在一偶发事件序列内以这种频率发生。
根据这种解释,“用这颗骰子下一次掷五的概率等于1/6”这陈述实际上不是一个关于下一次掷骰子的断言;宁可说,它是一个关于整个一类掷骰子的断言,下一次掷骰子不过是其中一个元素。这个陈述所说的不过是在这类掷骰子中得5的相对频率等于1/6。
按照这个观点,如果我们能够对数值概率陈述作出濒率阐述,这些陈述才是可接受的。不能作出频率解释的那些概率陈述,尤其是非数值概率陈述,常常被频率理论家回避。
下面我将尝试重新把概率理论作为一种(经过修改的)频率理论建立起来。因此我宣布我信仰客观解释;主要是因为我相信只有客观理论才能解释概率计算在经验科学中的应用。大家承认,主观理论能够给如何判定概率陈述的问题提供一个前后一致的解决办法;并且一般地说,它面临的逻辑困难比客观理论少。但是它的解决办法是:概率陈述是非常经验的;它们是重言的。当我们想起物理学利用概率论时,这种解决办法就证明是完全不能接受的了。(我摈弃主观理论的这种变种:认为客观频率理论应从主观假定中推导出来——也许利用Bernoulli定理作为“桥梁”;由于逻辑上的理由我认为这种纲领是不能实现的。)
49.机遇理论的基本问题
概率理论的最重要应用是用于我们可称之为“似相遇的”(chance-like)或“随机的”事件,或偶发事件。它们的特征是一种特殊的不可计算性,这使得人们经过许多次不成功的尝试后倾向于相信,一切已知的理性预测方法用于这些事件必定失败。可以说,我们感觉到除了先知以外没有一个科学家能够预测它们。然而正是这种不可计算性使我们得出这样的结论:概率的计算能够应用于这些事件。
如果我们接受主观理论,那么从不可计算性达到可计算性(即达到某种计算的可应用性)这个有点悖论性质的结论,确实不再具有悖论性质了。但是这种避免悖论的方法是极不令人满意的。因为它包含着这样的观点:概率计算与经验科学的所有其他方法相反,不是一种计算预测的方法。按照主观理论,它不过是一种使我们已知的东西或者更确切地说,使我们未知的东西实行逻辑变换的方法;因为正是在我们缺乏知识时我们实行这些变换。这种观念确实使悖论消解,但它不能解释被解释为频率陈述的无知陈述如何能够在经验上受到检验和得到验证。然而这正好是我们的问题。我们如何能够解释这个事实:我们可从不可计算性——即从无知——中作出能够解释为经验频率陈述的结论,并且尔后我们发现它们在实践中得到光辉的验证呢?
甚至频率理论直到现在还不能对这个问题——我将称之为机遇理论的基本问题——提供一个令人满意的解答。在第67节将表明这个问题与“收敛公理”有联系,后者是目前形式的这个理论的一个组成部分。但是在这个公理消除后,在频率理论框架内找到一个令人满意的解决办法是可能的。通过分析这样一些假定就会找到这种解答,这些假定使我们能够从单个偶发事件不规则序列推论到它们频率的规则性或稳定性。
50.von Mises 的频率理论
为概率计算的所有主要定理提供基础的频率理论首先由Richard von
Mises提出的。他的基本思想如下。
概率计算是似机遇的或随机的事件或偶发事件序列,即例如连续掷骰子那种重复性事件序列的理论。借助两个公理条件把这些序列定义为“似机遇的”或“随机的”:收敛公理(或极限公理),和随机公理。如果一个事件序列满足这两个条件,von
Mises就称它为一个“集合”(collective)。
大体上说,一个集会就是一个事件或偶发事件的序列,它在原则上可以无限地延续下去;例如掷骰子序列。假设骰子是破坏不了的。在这些事件中,每一个都有一定的特性和性质;例如可以掷个5,因而具有性质5。如果我们选取直到序列某一元素以前已出现的所有具有性质5的掷骰子次数,除以直到那个元素以前掷骰子的总数(即序列中它的基数),那么我们就获得直到那个元素以前的5的相对频率。如果我们确定了直到这个序列每个元素以前5的相对频率,我们就用这种方法获得一个新的序列——5的相对频率序列。这种频率序列不同于它与之相应的原先的事件序列,后者可称为“事件序列”或“性质序列”。
我选取我们称之为“二择一”(alternative)作为一个集合的简单例子。我们用这个词指假定只有两种性质的事件序列——例如掷一个钱币猜正反面的序列。一种性质(正面)用“1”表示,另一种性质(反面)用“0”来表示。于是事件序列(或性质序列)可用下式表示:
(A) 0 1 1 0 0 0 1 1 1 0 1 0
1 0……
与这种“二择一”相应——或更精确地说,与这种二择一的性质“1”相关——的是下列“相对频率序列”,或“频率序列”:
(A’)0 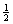 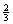 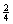 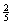 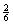 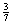 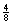 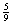 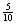 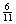 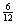 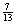  …… ……
收敛公理(或“极限公理”)假定,随着事件序列越来越长。频率序列将趋向一个确定的极限值。von
Mises使用这个公理是因为我们必须弄清楚我们能够借以工作的某个固定的频率值(即使实际的频率值有一些波动)。在任何集合中至少有两种性质;如果我们得到与某个集合所有性质相应的频率极限值,那么我们就得到集合的“分布”。
随机公理或有时称之为“排除赌博系统原理” (the
principle of the excluded gambling
system),是打算用来为序列的似机遇性质提供数学表现。显然,如果掷硬币的序列有规律性,比方说在每三次掷正面后就出现反面相当有规律,那么一个赌徒就会用某种赌博系统来改善他的运气。随机公理就一切集合假定,不存在能够成功地应用于这种集合的赌博系统。它假定,不管我们可以选取何种赌博系统以选择认为有利的掷猜(tosses),我们将发现,如果赌博有足够长的时间继续下去,认为有利的掷猜序列中的相对频率接近的极限值与所有掷猜序列的极限值是一样的。因此存在着一种赌徒能借以改善他运气的赌博系统的序列不是von
Mises意义上的集合。
对于von Mises来说,概率是“集合中相对频率极限度”的另一个术语。所以概率概念仅应用于事件序列;从Keynes等人的观点看来,这样的限定大概是完全不能接受的。对于批评他的解释太窄的人,von
Mises的回答是强调科学的使用概率(例如在物理学中)与一般的使用概率之间的不同。他指出要求定义恰当的科学术语非要在一切方面去适应不确切的、前科学的用法是个错误。
按照von Mises的意见,概率计算的任务只不过在于此:从具有某些给定“初始分布”(initial
distributions)的某些给定“初始集合”(initial collectives)推论出具有“导出分布”(derived
distributions)的“导出集合”(derived collectives);简言之,根据给定的概率计算出那些没有给定的概率。
von Mises把他的理论的独特特点概括为四点:集合概念先于概率概念;定义概率概念为相对频率的极限值;提出随机公理;以及规定概率计算的任务。
51.新的概率理论计划
von Mises提出的两条公理或公设以定义集合概念曾遇到强烈的批评——我认为这个批评不是没有道理的。特别是反对把收政公理和随机公理结合起来,理由是不允许把极限或收敛的数学概念应用于按照定义(即由于随机公理)必定不服从任何数学规则或定律的序列。因为数学极限值不过是决定序列的数学规则或定律的特有性质。数学极限值不过是这种数学规则或定律的一种性质,如果任意选定一个接近于零的分数,序列中都有一个元素,使得在它之后的所有元素与某个一定的值的差小于这个分数——于是这个值称为它们的极限值。
为了对付这些反对意见,有人建议不要把收敛公理和随机公理结合起来,仅假定收敛,即被限值的存在。至于随机公理,建议或者全然放弃它(Kamke),或者用较弱的要求代替它(Reichenbach)。这些意见的前提是认为引起麻烦的是随机公理。
与这些观点相对照,我倾向于责怪收敛公理不亚于责怪随机公理。因此我认为有两项任务要做:改进随机公理——主要是一个数学问题;以及完全消除收敛公理——认识论家特别关心的一个问题(参阅第66节)。
下面我首先讨论数学问题,然后讨论认识论问题。
这两项任务中的第一项,即数学理论的重建,其主要目的是从一个修改了的随机公理推导出Bernoulli定理——第一个“大数定律”;修改为实现这个目的所需,不要求更多。更确切地说,我的目的是推导出二项式公式(Binomial
Formula,有时称为“Newton公式”),我称为“第三式”。因为能用通常的方法从这个公式中获得Bernoulli定理和概率论的其他极限定理。
我的计划是首先制定一个有穷类(finite class)的频率理论,并且尽量在这个框架内发展这个理论——即直至推导出(“第一”)二项式。这个有穷类频率理论原来是类理论(thetheory
of classes)一个十分基本的部分。它之得到发展只是为了获得讨论随机公理的基础。
接着我将通过引入收敛公理的老方法进而到无穷序列,即能够无限延续的事件序列,因为我们需要它来讨论随机公理。在推导出和考察Bernoulli定理之后,我将考虑如何能消除收敛公理,以及哪一类公理系统我们应该作为结果保留下来。
在数学推导的过程中,我将使用三个不同的频率符号:F”示有穷类的相对频率;F’示无穷频率-序列相对频率的极限值;最后F示客观额率,即在“不规则”或“随机”或“似机遇”序列中的相对频率。
52.有穷类内的相对频率
让我们考虑一类α的有穷数目的偶发事件,例如昨天用这粒特定的骰子掷猜这类偶发事件。设这类α为非空类(non-empty),可以说它起着参考系的作用,将称之为(有穷的)参考类(reference-class)。属于α的元素数目,即它的基数,用“N(α)”表示,读作“α数”。另一类β,可以是有穷的,也可以不是有穷的。我们称β为性质类(property-class)。例如它可以是所有掷5的类,或(如我们将要说的)所有具有性质5的掷猜类。
属于α又属于β的那些元素类,例如昨天用这粒特定的骰子掷并有性质5的掷类被称为α和β的乘积类(product-
class),用“α·β”表示,读作“α和β”。由于α·β是α的子类,它至多能含有有穷的元素数(它可以是空类)。α·β中的元素数用“N(α·β)”表示。
当我们用N表示(有穷)的元素数时,用F”示相对频率。例如,“在有穷参考类α内性质β的相对频率”写作“αF”(β)”,可读作“β的α频率”。我们现在能定义
(定义1) αF”(β)=N(α·β)/N(α)
根据我们的例子这意味着:“昨天用这骰子掷时出现5的相对频率,按照定义等于昨天用这骰子掷5的数被昨天用这骰子掷的总数来除所得的商。”
从这个颇为平凡的定义中,能够十分容易地推导出有穷类中频率计算的定理(更具体地说,一般乘法定理;加法定理;以及除法定理,即Bayes规则)。在这种频率计算的定理中,以及在一般的概率计算中,其特征是基数(N数)从不在其中出现,出现的是相对频率,即比值,或F数。N数仅发生在一些基本定理的证明中,这些基本定理是直接从这个定义中演绎出来的;但N数并不发生在定理自身中。
在这里用一个十分简单的例子来说明对此应作如何理解。让我们用“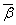 ”(读作“β的补数”或简单地读作:“非β”)来表示不属于β的一切元素类。于是我们可写出: ”(读作“β的补数”或简单地读作:“非β”)来表示不属于β的一切元素类。于是我们可写出:
αF”(β)+αF”( 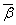 )=1
)=1
虽然这个定理仅包含F数,它的证明要利用N数。因为这定理认定义(1)中得出,借助于来自断言N(α·β)十N(α·β)=N(α)的类的计算的一个简单定理。
53.选择、独立、无影响、无关
在能够用有穷类相对频率作的运算中,选择(selection)的运算对以下所述有特殊重要性。
设给定一个有穷参考类α,例如一只匣子中的钮扣类,以及两个性质类,β(比方说,红钮扣)和γ(比方说,大钮扣)。我们现在可把乘积类α·β看作一个新的参考类,并提出α·βF”(γ)值的问题,即在新的参考类内γ的频率的问题。新的参考类α·β可称为“从α中选择β元素的结果”或“按照性质β从α中选择”;因为我们可以想到它是通过从α中选择那些具有性质β(红)的一切元素(钮扣)。
γ发生在新的参考类α·β中的频率与发生在原先的参考类α中的频率相同,这恰恰是可能的;即
α·βF”(γ)=αF”(γ)是正确的。在这种情况下,我们(遵循Hausdorff)说性质β和γ“在参考类a内是相互独立的”。独立关系是三项关系,在性质β和γ上是对称的。如果两种性质α和β在参考类α内是(相互)独立的,我们也可说性质γ在α内不受β元素的选择的影响;也许可说参考类α,就性质γ而言,不受按照性质β所作的选择的影响。
β和γ在α内相互独立或不受影响也可——按照主观理论的观点——解释如下:如果我们被告知类α的某一特定元素具有性质β,那么这个信息是无关的,如果β和γ在α内是相互独立的话;也就是对于这个元素是否也有性质γ这个问题是无关的。如果另一方面我们知道,γ更经常(或不那么经常)发生在子类α·β(已根据β从α中选择出来)中,那么某个元素有性质β的信息对于这个元素是否也有性质γ的问题便是有关的了。
54.有穷序列、顺序选择和邻域选择
设有穷参考类α的元素是编了号的(例如盒子中的每一个钮扣都写上一个数目),并且把它们按照序数排列成序列。在这种序列中我们可以区分出两类具有特殊重要性的选择,即按照元素的序数进行选择,或简称顺序选择,以及按照它的邻域进行选择。
顺序选择是根据依赖于元素序数的性质β从序列α中进行选择,元素的选择必须根据序数决定。例如β可以是性质偶数(even),因此我们从a中选择的一切元素,其序数是偶数。因此选择出来的元素形成一个所选子序列(selected
sub-sequence)。如果性质γ独立于根据β的顺序选择,那么我们也可说,顺序选择对γ而言是独立的;或者我们也可说序列α就γ而言,不受β元素的选择的影响。
邻域选择之有可能是由于这个事实:在把元素排列为编号序列时,某些邻域关系就形成了。这使我们例如有可能选择那些其直接先行者具有性质γ的所有成员;或者比方说,选择那些其第一和第一个先行者,或其第一个后续者具有性质Y的所有成员,如此等等。
因此如果我们有一个事件序列——比方说掷钱币猜正反面——,我们就必须区分两类性质:如“正面”或“反面”那样一些的主要性质,这些性质属于与其在序列中位置无关的每一个元素;以及如“偶数”或“反面的后续者”等那样一些次要性质,这些性质是一个元素由于它在序列中的地位而获得的。
具有两个主要性质的序列称为“二择一”。正如von Mises业已表明的(如果我们小心仔细),有可能把概率论的基本点发展为二择一理论,而不牺牲普遍性。用“1”和“0”表示二择一的两种主要性质,每一种二择一可表示为许多1和0的序列。
一种二择一的结构可以是有规律的,或者它也可能是多少不规则的。下面我将更周密地研究某些有穷二择一的这种规律性或不规则性。
55.有穷序列的n-自由度
让我们以有穷二择一α为例,它由一个个1和0组成,有规律地排列如下:
(α)
1 1 0 0 1 1 0 0 1 1 0 0 1 1 0
0……在这种二择一中,我们有均等的分布,即1和0的相对频率是均等的。如果我们用“F”(1)”示性质1的相对频率,用“F”(0)”示性质0的相对频率,我们可写:
(1)αF”(1)=αF”(0)=1/2
现在我们从α中选择(在α序列内)具有直接接在1后面的邻域性质的所有项。如果我们用“β”表示这种性质,我们可称为所选子序列“α·β“。它有这样的结构:
(α·β)
1 0 1 0 1 0 1 0 1 0……
这个序列又是具有均等分布的一种二择一。而且,1和0的相对频率都没有变化;即
(2)α·βF”(1)=αF”(1);α·βF”(0)=αF”(0)
用第53节采用的术语,我们可以说二择一α的主要性质不受根据性质β作的选择的影响;简言之,α不受根据β作的选择的影响。
由于α的每一个元素或具有性质β(即是1的后续者)或是0的后续者,我们可用“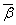 ”表示后一性质。如果我们现在选择具有性质 ”表示后一性质。如果我们现在选择具有性质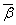 的元素,我们得到这样的二择一:
的元素,我们得到这样的二择一:
(α·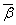 )
0 1 0 1 0 1 0 1 0 1 0…… )
0 1 0 1 0 1 0 1 0 1 0……
这个序列离均等分布稍有偏差,因为它的始末都是0(因为均等分布a本身以“0’0”结尾)。如果a有2000个元素,那么α·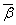 将有500个0,只有499个1。这些离均等分布(或其他分布)的偏差只是因第一个元素或最后一个元素而引起的,可通过使序列足够长而使这些离差变得如我们喜欢的那么小。由于这个理由在下面我们将置这些偏差于不顾;尤其是我们研究的是无穷序列,在那里这些离差就消失了。因此,我们说,二择一α·β有均等的分布,并且二择一α不受有性质 将有500个0,只有499个1。这些离均等分布(或其他分布)的偏差只是因第一个元素或最后一个元素而引起的,可通过使序列足够长而使这些离差变得如我们喜欢的那么小。由于这个理由在下面我们将置这些偏差于不顾;尤其是我们研究的是无穷序列,在那里这些离差就消失了。因此,我们说,二择一α·β有均等的分布,并且二择一α不受有性质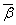 的元素的选择的影响。结果,α,或更确切地说,α的主要性质的相对频率都不受根据β和根据 的元素的选择的影响。结果,α,或更确切地说,α的主要性质的相对频率都不受根据β和根据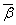 作的选择的影响;所以我们可以说,α都不受根据直接先行者的性质所作的每一种选择的影响。 作的选择的影响;所以我们可以说,α都不受根据直接先行者的性质所作的每一种选择的影响。
显然,这种无影响是由于二择一α结构的某些方面所致;这些方面可把α与其他二择一区分开来。例如,二择一α.β和α.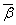 并非不受根据先行者的性质所作的选择的影响。 并非不受根据先行者的性质所作的选择的影响。
现在我们可以研究二择一α,看看它是否也不受其他选择,尤其是根据一对先行者的性质所作的选择的影响。例如,我们可从α中选择那些是一对1,1的后续者的所有元素。并且我们马上看到α并非不受四种可能的对即1,1;1,0;01;0,0中任何一对后续者的选择的影响。在这些情况下,得到的子序列都没有均等分布;反之,它们全都由不间断的块(blocks,或“反复”iterations)组成,即只由1,或只由0组成。
α不受根据单个先行者作的选择的影响,但是并非不受根据成对先行者的选择的影响,这个事实可用主观理论的观点表述如下。关于α中任何元素一个先行者性质的信息,对于这个元素的性质问题是无关的。另一方面,关于元素的成对先行者的性质的信息则是高度有关的;因为给定α据以建立的定律,它使我们能够预测所讨论的元素的性质:关于元素成对先行者性质的信息,可以说给我们提供演绎出预测所需的初始条件。(a据以建立的定律要求一对性质作为初始条件;因此就这些性质而言,它是“二维的”。详细说明一种性质仅是在成为复合时作为初始条件不充分时才是“无关的”。参阅第38节。)
我没有忘记因果性——原因和结果——概念与预测的演绎的关系是多么密切,同时我要利用下列术语。以前作出的关于二择一α的断言:“α不受根据单个先行者作的选择的影响”,我现在用下列说法来表示:“α不受单个先行者任何后效的约束”,或简言之,“α的自由度为1(1-free)”。不像以前那么说α“不受(或受)根据成对先行者所作的选择的影响”,我现在说:“a不受(或受)成对先行者后效的约束”,或简言之,“α的自由度是(不是)2”。
用自由度为1的二择一作为我们的原型,我们现在能够容易地建立也具有均等分布的其他序列,这些序列不仅不受一个先行者的后效约束,即(像α一样)自由度为1,而且还不受一对先行者后效的约束,即自由度为2;此后,我们可以继续达到自由度为3等等的序列。这样把我们引导到对下述是基本的一般概念。这就是不受直至某个数n的一切先行者后效约束的自由度概念;或者如我们将要说的,n-自白度概念。更精确地说,我们称一个序列“自由度为n”,当且仅当它的主要性质的相对频率是“n重无影响”,即不受根据单个先行者和根据成对先行者和根据三个一组的先行者……和根据n个一组先行者作的选择的影响。
自由度为1的二择一α可以用重复任何倍数的生成周期(generating
period)。
(A)
1 1 0 0……
来建立。同样我们获得具有均等分布的自由度为2的二择一,如果我们把
(B)
1 0 1 1 1 0 0 0……
作为它的生成周期,自由度为3的二择一从生成周期
(C)
1 0 1 1 0 0 0 0 1 1 1 1 0 1 0 0……
中获得,而自由度为4的二择一从生成周期
(D)
0 1 1 0 0 0 1 1 1 0 1 0 1 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 1……
中获得。将会看到:面临一个不规则序列的直觉印象随它n自由度的数n的增长而越强烈。
具有均等分布的一个具n自由度的二择一的生成周期必须包含至少2n+1个元素,作为例子给定的周期,当然可以开始于不同的位置;(C)例如可从它的第四个元素开始,于是我们获得的不是(C),而是
(C’)
1 0 0 0 0 1 1 1 1 0 1 0 0 1 0 1……
有使序列的n-自由度不变的其他变换。为每一个数目n建立n-自由度序列生成周期的方法则在别处描述。
如果我们把下一生成周期的最初的n个元素加在一个自由度为n的二择一上,于是我们得到一个长度为2[n+1]+n的序列。除了其他性质外,这个序列还有以下的性质:n+1个0和1的每一种排列,即每一个可能的n+1个组,至少在其中发生过一次。
56.节段序列 二项式的第一形式
给定一个有穷的序列α,我们称由n个连续元素组成的α的子系列为‘’α的n长度节段”;或更简单地说,“α的n-节段”。如果除了序列α以外,还给定某个定数n,那么我们能够把α的n-节段排列在一个序列中——α的n-节段序列。给定一个序列α,我们就可以从α的最初的n个元素的节段开始这种方式,建立一个新的序列,即α的n-节段序列。其次是α的2到n+1的元素的节段。一般地说,我们把α的从x到x+n-1的诸元素组成的节段看作新序列的第x个元素。如此获得的新序列可称为“α的交迭n-节段(overlapping
n一segments)序列”。这个名称表示,新序列的任何两个连续元素(即节段)以这种方式交迭;使它们共有原先序列α的n-1元素。
现在我们通过选择可以从一个交迭节段的序列中,获得其他序列,尤其是毗邻n-节段(adjoining
n-segments)的序列。
一个毗邻n-节段序列只含这样一些n-节段,它们在不交迭的α中,互相直接接续。例如开始也许是原先序列α的编号为1至n的元素的n-节段,续在后面的是n+1至2n,2n+1至3n如此等等的元素的n-节段。一般来说,一个毗邻节段的序列将以α的第k个元素开始,而它的节段将包含α的编号为直至n+k-1,n+k至2n+k-1,2n+k至3n+k-1如此等等的元素。
下面将用“α(n)”示α的交迭n-节段的序列,用“αn”示毗邻n-节段序列。
现在让我们更详细一点考虑交迭节段α(n)的诸序列。这样一种节段的每一个元素是α的一个n-节段。我们可以把例如组成节段的n个一组的有序的0和1看作是α(n)一个元素的主要性质。或者我们可以更为简单地把它的1的数目看作是这个元素(不管1和0的次序)的主要性质。如果我们用“m”表示1的数目,则显然m≤n。
现在我们又从每一个序列α(n)得到一个二择一。如果我们选择一个特定的m(m≤n),并将性质“m”赋予序列α(n)的正好有m个1(所以有n-m个0)的每一个元素,并且把性质“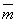 ”(非m)赋予α(n)的所有其他元素的话。因此α(n)的每一个元素必定有这两个性质中的一个或另一个。 ”(非m)赋予α(n)的所有其他元素的话。因此α(n)的每一个元素必定有这两个性质中的一个或另一个。
现在让我们再次设想,给定一个具有主要性质“1”和“0”的一个有穷二择一。设1的频率αF”(1)等于p,0的频率αF”(0)等于q。(我们设分布是不均等的,即p≠q。)
现在让这个二择一α至少有n-1个自由度(n是任意挑选的自然数)。于是我们可向下列的问题:性质m在序列α(n)中出现的频率是多少?换言之,α(n)F”(m)的值是多少?
除了α至少有n-1个自由度外,我们什么也不假定,我们就能用初等算术解决这个问题。答案包含在下列公式中:
(1)α(n)F”(m)=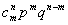
“二项”式(1)的右边是由Newton在论述有关别的问题时提出的(有时称为Newton公式)。我将称它为“二项式的第一形式”。
由于推导出了这个公式我就不再在有穷参考类内考察频率理论。这个公式将提供给我们一个基础来讨论随机公理。
57 无穷序列 频率的假说性估计
把为n-自由度有穷序列获得的结果推广到用生成周期(参阅第55节)定义的n-自由度无穷序列是十分容易的。起着参考类(我们的相对频率与此有关)作用的一个无穷的元素序列可称为“参考序列”。它多少与von
Mises意义上的“集合”相对应。
n-自由度的概念以相对频率的概念为前提;因为n-自由度的定义要求不受影响——不受根据一定的先行者所作的选择的影响——的是一种性质在其中发生的相对频率。在我们讨论有穷序列的定理中,我将暂时使用(直到第64节)相对频率极限值(用F’表示)概念代替有穷类的相对频率(F”)。只要我们把自己限于根据某个数学规则建立的参考序列,这个概念的使用就不会发生问题。对于这些序列我们总可以确定相应的相对频率序列是否是收敛的。相对频率极限值概念只是在没有数学规则只有经验规则(与例如钱卜序列有关的)的序列的情况下才会引起麻烦;因为在这些情况下,极限值概念是未定义的(参阅第51节)。
建立序列的数学规则的一个例子如下:“序列α的第n个元素应该是0,当且仅当n可被4除”。它定义的无穷二择一是
(α)
1 1 1 0 1 1 1 0……
其相对频率的极限值αF’(1)=3/4; αF’(0)=1/4。借助数学规则用这种方法定义的序列我简称为“数学序列”。
与之相对照,建立经验序列的规则是例如“序列α的第n个元素将是0,当且仅当硬币c的第n次掷猜出现反面时”。但是经验规则不一定总是定义随机性质的序列。例如,我应该把下列规则称为经验规则:“序列的第n个元素将是1,当且仅当第n秒(从某个零时算起)时,发现摆p摆到这标记的左方时”。
这个例子表明有时——例如根据与摆有关的一些假说和测量——可用数学规则代替经验规则。用这种方法我们会找到一个数学序列,它以按我们的目的也许使我们满意,也许不能使我们满意的精确度接近于我们的经验序列。有可能(我们的例子可用来建立这种可能)获得一个其各种频率接近于那些经验序列的频率,在我们目前的情况下具有特殊的意义。
我把序列分为数学序列和经验序列时,我利用的是“内包”上的差别,不是“外延”上的差别。因为如果用“外延”方法,即用一个接一个地列举其元素的方法使我们得一个序列--因此我们就只能知道它的一个有穷的片段,一个有穷的节段,不管它有多长——,那么就不可能根据这个节段的性质确定其一部分的序列是学序列还是经验序列。仅当给定一个建构规则——即“内包”规则—一时,我们就能判定一个序列是否是数学的还是经验数的。由于我们希望借极限值(相对频率)概念之助处理我们的无穷序列,我们必须把我们的研究限于数学序列,实际上就是限于相应的相对频率序列是收敛的那些数学序列。这种限制等于引入收敛公理。(与这公理有关的问题到第63-66节再讨论,因为与“大数定律”一起讨论它们比较方便。)
因此我们将只谈数学序列。然而我们将只谈那些数学序列:我们期望或推测它们就频率而言接近于具有似机遇或随机性质的经验序列,因为它们是我们的主要兴趣所在。但是期望或推测一个数学序列,就频率而言它接近于经验序列,不过是提出一个假说——一个关于经验序列频率的假说。
我们对经验随机序列的频率的估计是假说这一事实,对我们用以计算这些频率的方法没有任何影响。显然,在有穷类方面,它对我们如何获得我们的计算由此开始的频率,丝毫没有关系。这些频率可借实际计算获得,或根据一条数学规则,或根据某种假说获得。或者我们简直可以虚构一些频率。在计算频率时我们接受某些频率作为给定的,并从中推导出其他频率。
无穷序列中的概率估计同样如此。因此关于我们频率估计的来源问题不是一个频率计算问题;然而这并不是说把这个问题从我们关于概率论问题的讨论中排除出去。
在无穷经验序列的情况中,我们能区分出我们假说性频率估计的两种主要“来源”——就是说两种方法,我们用这两种方法就可估计出频率。一是基于“均等-机遇假说”(equal
chance hypothesis),(或等概率假说equi-probability
hypothesis)的估计,另一是基于统计结果的外推(extrapolation of statisticalfndings)。
我用“均筹-机遇假说”,是指这样一种假说,它断言各种主要性质的概率是均等的:它是断言均等分布的假说。均等-机遇假说常常基于对称性的考虑。最典型的例子是掷骰子时均等频率的推测,其根据是立方体六面的对称性和几何等值。
至于基于统计学外推的频率假说,死亡率的估计提供一个很好的例子。在这里关于死亡率的统计资料是用经验查明的,并且根据过去的趋势将继续足十分接近稳定的,或者它们不会有很大变化——至少在最近时期内——的假说从已知事例,即从已用经验加以分类和计算的偶发事件外推到未知事例。
具有归纳主义倾向的人容易忽视这些估计的假说性质,他们会把假说性估计,即基于统计外推的频率预测同它们的经验“来源”之——过去的偶发事件和偶发事件序列的分类与实际计算混为一谈。往往提出这样的主张;我们从已加以分类和计算的过去的偶发事件(如死亡统计)中“推导出”概率估计——即频率预测。但是从逻辑观点看,这个主张并没有得到证明。我们根本没有作什么逻辑推导。我们已经做的是提出一个不可证实的假说,这个假说在逻辑上是永远得不到证明的,这个假说就是推测频率仍将稳定不变,因此允许外推。甚至均等-机遇假说也被一些相信归纳逻辑的人认为是“经验上可推导的”,或“经验上可说明的”,他们认为这些假说基于统计经验,即基于经验上观察到的频率。然而就我来说,我相信,我们在作出这种假说性估计时,往往单独爱关于对称意义的想法以及类似的考虑的引导。我看不出有任何理由为什么这些推测应该只是由于积累大量归纳观察而产生的。然而,我并不赋于我们估计的起源或“来源”这些问题以很大意义(参阅第2节)。我认为,更重要的是对这个事实要十分清晰,即频率的一切预测性估计,包括我们从统计外推中得到的频率——当然还有所有与无穷经验序列有关的频率——总是纯粹的推测,因为它总是超出我们有权根据观察肯定的任何东西。
我对均等-机遇假说和统计外推的区分与“先验”和“后验”概率的经典区分是完全符合的。但是由于这些术语是用于如此多的不同意义。而且由于这些术语因哲学上的联想而被严重玷污,最好还是避免用它们。
我在下面考察随机公理时,将试图寻找逼近随机经验序列的数学序列;这就是说我将考察频率假说。
58 随机公理的考察
顺序选择(即按位置选择)的概念和邻域选择的概念均已在第55节中引入和说明。我现在将借助这些概念检查vonMises的随机公理——排除赌博系统原理——以希望找到一个能代替这个公理的较弱的要求。在von
Mises的理论中,这个公理是他的集合概念的定义的一部分:他要求一个集合中频率的极限一定要对任何种类的系统选择(systematic
Selection)不敏感(他指出,赌博系统总是可被认为是一种系统选择。)。
对这个公理提出的大多数批评集中于它的表述的相对不重要的和表面的方面。这与下列事实有关,即在各种可能的选择中,会有这样的选择:比方说选择那些接近5的掷;显然在这种选择内,5的频率会与在原先序列内5的频率迥然不同。这就是为什么von
Mises在他的随机公理表述中谈到他所说的“选择”或“选取”是“独立于”掷的“结果”,因而不用所选元素的性质去定义。但是只要指出我们可以根本不用成问题的措词来表述von
Mises的随机公理,就可以完全答复针对这种表述的许多非难。因为例如我们可以表述如下:在一个集合中频率的极限一定都不受顺序选择和邻域选择的影响,而且也不受可用作赌博系统的这两种选择方法的所有组合的影响。
上述困难随这个表述而消失。然而其他困难仍保留。因此也许不可能证明,借助如此强的随机公理定义的一个集合概念,不是自相矛盾的;换言之,不可能证明“集合”的类不是空的。(Kamke曾强调证明这一点的必要)至少,建构某个集合的例子,并用这种方式说明集合的存在,这似乎是不可能的。这是因为满足一定条件的某一无穷序列的例子只可能由数学规则来提供。但是对于von
Mises意义上的集合,根据定义不可能有这种规则,因为能够把任何规则都用作一种赌博系统或选择系统。如果所有可能的赌博系统都被排除,这种批评确实是无法驳斥的。
然而也可提出另外的异议来反对排除所有赌博系统的概念:它的要求实在太多了。如果我们要使某个陈述系统公理化——在这个场合是概率计算定理,尤其是特殊的乘法定理或Bernoulli定理——,那么所选的公理不仅应该对系统定理的推导是充分的,而且也是(如果我们能这样推导出定理)必要的。然而可以表明排除所有选择系统对Bernoulli定理及其系统定理是不必要的。要求排除特殊类的邻域选择是十分充分的:它是以要求序列应该不受根据任意选取的n个一组的先行者所作的选择的影响;也就是说,它应该有n个自由度,不受每个n的后效的约束,或简言之,它应该是“绝对自由的。”
所以我建议用不那么严格的“绝对自由”的要求(对每一个n有n-自由度的意义上)来代替von Mises的排除赌博系统原理,并且相应地把似机遇的数学序列定义为满足这个要求的序列。其主要优点是不排除所有赌博系统,因此有可能提供建构在我们的意义上“绝对自由的”序列的数学规则,从而有可能建构实例。因此也就满足了上面讨论的Kamke的异议。因为我们现在能够证明似机遇数学序列的概念不是空的,所以是前后一致。
也许有点奇怪:我们应该试图借助必须符合最严格规则的数学序列来勾划机遇序列极不规则的特点。von Mises的随机公理起初似乎使我们的直觉更为满意。一个机遇序列必定是完全不规则的,因此只要我们继续努力试图通过把这个序列延伸得足够长来证伪这个推测的话,任何推测的规则性一定会在序列的后面部分遇到失败,知道这一点是颇为令人满意的。但是这个直觉的论证也有利于我的建议。因为如果机遇序列是不规则的,那么,不容置疑,它们就不会是某种特殊类型的规则序列。而我们的“绝对自由”要求不过是排除一种特殊类型的规则序列,尽管是一种重要的类型。
它是一种重要的类型这一点可以从这个事实中看出,即根据我们的要求不言而喻地排除下述三种典型的赌博系统(参阅下一节)。首先我们排除“正态的”或“纯粹的”邻域选择,在其中我们根据邻域的某种恒定的特征进行选择。其次,我们排除“正态的”顺序选择,这种选择选取的元素,它们的间距是恒定的,例如标号为是k,n+k,2n+k……等等的元素;最后,我们排除这两种类型选择的许多组合(例如一切第n个元素的选择,假如它的邻域具有某种具体的恒定特征)。所有这些选择的独特性质是,它们与序列的绝对的第一元素无关;如果原先的序列从另一个(相应的)元素开始标号,它们就可产生同样的所选的子序列。因此被我的要求排除的赌博系统是那些无需知道序列的第一元素而可使用的赌博系统。被排除的系统总涉及某些(线性)变换。它们是简单的赌博系统。(参阅第43节)。我的要求不予排除的只是涉及诸元素与绝对的(初始的)元素间有绝对距离的赌博系统。
对一切n有自由度n——“绝对自由”——的要求也与我们大多数自觉地或不自觉地认为对机遇序列也适用的东西完全一致;例如一粒骰子下一次掷的结果不依赖以前几次掷的结果(掷以前摇摇骰子的做法就是想要保证这种“独立性”)。
59.似机遇序列 客观概率
鉴于我已说过的那些东西,我现在提出下列定义。
我们说一个事件序列或性质序列,尤其是一个二择一,是“似机遇”或“随机的”,当且仅当它的主要性质的频率极限是“绝对自由的”,即不受根据任何n个一组的先行者的性质所作的一切选择的影响。与随机的序列相应的频率极限被称为在有关序列内该性质的客观概率;用F表示。这也可表述如下。设α为具有主要性质B的似机遇或似随机序列;这时下式成立:
αF(β)=αF’(β)
现在我们必须证明我们的定义足以推导出数学概率论的主要定理,尤其是Bernoulli定理。随后——在第64节——这里给定的定义将予以修改使之独立于频率极限的概念。
60.Bernoulli问题
在第56节提到的第一个二项式公式,即
(1)α(n)F”(m)=
适用于交迭节段的有限序列。它可根据这样的假定推导出来,即有限序列α至少有n-1个自由度。根据同样的假定,我们直接获得一个有限序列的正好相应的公式;那就是说,如果α是有限的,并且至少有n-1个自由度,那么
(2)α(n)F’(m)=
由于似机遇序列是绝对自由的,即对于每一个n有n个自由度,公式(2),即第二个二项式公式也必须适用于那些序列;并且确实它必须适用于它们,不管我们选择的n的值是多少。
下面我们将只涉及似机遇序列,或随机序列(如在前节中定义的那样)。我们就要证明,对于似机遇序列,除了公式(2),第三个二项式公式(3)也必定适用;这个公式是
(3)αnF(m)=
公式(3)在两个方面不同于公式(2):第一,它所断言的涉及毗邻节段αn的序列,不是交迭节段α(n)的序列。第二,它不包含符号F’,而包含符号F。这意味着,根据蕴涵它断言邻近节段序列也是似机遇或随机的;因为从F,即客观概率的定义仅涉及似机遇序列。
(3)所回答的在邻近节段序列中性质m的客观概率问题——即αnF(m)的值的问题——,我效法von
Mises,称之为“Bernoulli问题。对于这个问题的解决,从而对于第三个二项式公式(3)的推导,假定α是似机遇或随机的也就够了。(我们的任务等于说明特殊的乘法定理适用于一个随机序列α的毗邻节段序列。)
公式(3)的证明可用两步实现。首先,我们证明公式(2)不仅适用于交迭节段α(n)的序列,而且也适用于毗邻序列αn的序列。第二,我们证明后者是“绝对自由的”。(这两步的次序可以颠倒,因为交迭节段α的序列肯定不是“绝对自由的”;事实上,这种序列提供了一个可称之为“具有后效的序列”的典型例子。)
第一步。毗邻节段αn的序列是α(n)的子序列,它们可通过正态顺序选择从α(n)中获得。因此如果我们能证明在交迭序列α(n)F’(m)中频率的极限不受正态顺序选择的影响,我们就是已经采取了第一步(以及甚至走得更远一点);因为我们将证明这个公式:
(4)
αnF’(m)=α(n)F’(m)
我将首先以n=2为例概述这个证明;即我将证明
(4a)
α2F’(m)=α(2)F’(m) (m≤2)
为真;因此很容易概括这个公式以适用于一切n。
从交迭节段α(2)的序列中,我们能够选择毗邻节段的两个以及仅仅两个不同的节段α(2);一个用(A)表示,包含α(2)的第一,第三,第五……节段,即由数1,2;3,4;5,6;……组成的α的元素对另一个用(β)表示,包含α(2)的第二,第四,第六,……,节段,即由数2,3;4,5;6,7;……等组成α的元素对。现在假定公式(4a)不适用于两个序列中的一个,(A)或(B),结果节段(即对)0,0太经常出现在比方说序列(A)中;于是在序列(B)中必须出现一个余离差(complementary
deviation);即节段0, 0将不很经常出现(“太经常”,或“不很经常”是与二项式公式相比较而言的)。但是这与所假定的α的“绝对自由”是矛盾的。因为如果0,0对在(A)中出现比在(B)中更经常,那么在α的足够长的节段中,0,0对在某些表示特征的间距内出现比在其他间距内出现更经常。如果0,0对属于两个α2序列中的一个,更为经常出现的间距就是那些占优势的间距,如果0,0对均属于两个α2-序列,不那么经常出现的序列就是那些占优势的序列。但是这与所假定的α的“绝对自由度”是矛盾的;因为根据第二个二项式公式,α的“绝对自由度”意味着,在任何α(n)序列中一个特定的长度为n的序列出现的频率只依赖在该序列中出现的1和0的数目,而不是依赖它们在序列中的排列。
这证明(4a);由于这个证明能容易推广到任何n,(4)也就得到证明;这就完成了证明的第一步。
第二步。αn序列是绝对自由的这一事实可用一个类似的论据来说明。我们仍可以首先只考虑α2序列;而就这些序列而言,开始只会证明它们的自由度为1。设两个α2序列中的一个,即节段(A)并不是自由度为1。那么在(A)中,在至少由两个元素(一个特定的α对)组成的一个节段之后,比方说在0,0节段之后,另一个节段比方说1,1,必须比如果(A)是“绝对自由的”时更为经常地跟随着;这就是说,节段1,1出现在根据先行节段0,0从(A)中选择的子序列中的频率比二项式公式使我们期望更大。
然而,这个假定与序列α的“绝对自由度”是矛盾的。因为如果节段1,1在(A)中跟随节段0,0过分经常,那么通过补整(compensation),相反情况也必须出现在(B)中;因为否则四个一组0,0,1,1在α的一个足够长的节段中,会太经常地出现在某些特征性间距内——即在如果所说的两对属于同一α2序列就会占优势的那些间距内。此外,在其他特征性间距内,四个一组会不那么经常地出现——即在那些如果它们均属于两个α2序列就会占优势的间距内。因此我们面临的正好是与以前同样的情况;而且我们能用类似的考虑证明,假定事件在一些特有的间距内优先发生,是所假定的α的“绝对自由度”是不相容的。
这个证明又可加以推广,结果我们可以说α序列不仅自由度为1,而且对每一个n,自由度为n,因而它们是似机遇的,或随机的。
这就完成了我们对这两步的概述。因此我们现在有权在(4)中用F代替F’;这就是说,我们可以同意这个主张:第三个二项式公式解决了Bernoulli问题。
顺便说一句,我们已证明交迭节段的序列α(n)不受正态顺序选择的影响,只要α是“绝对自由”时。
这同样适用于毗邻节段序列αn,因为从αn中作的任何一个正态顺序选择可被认为是从α(n)中作正态顺序选择;所以它必须应用于序列α本身,因为α与α(1)和α1都是等同的。
因此我们也还证明了,不受正态顺序选择的影响是从“绝对自由度”——它意指不受某一特殊类型的邻域选择的影响——中得出的必然结论。容易看出,更进一步的结论是不受任何“纯”邻域选择(即根据它的邻域的某个恒定的特征——不随元素序数而变化的特征——进行选择)的影响。最后它的必然结论是“绝对自由度”蕴含着不受这两类选择的所有组合的影响。
61.大数定律(Bernoulli定理)
在假定我们能使n趋向极限。即n→∞的条件下,Bernoulli定理,或(第一)“大数定律”可以用纯粹数学的推理从第三个二项式方式中推导出来。所以它能断言的只是无限的序列α;因为正是仅仅在这些序列中αn-序列的n-节段长度能无限增加。并且它能断言的只是这些“绝对自由”的序列,因为正是仅在假定对每一个n自由度为n的条件下,我们能使n趋向极限,n→∞。
Bernoulli定理提供了十分类似我曾(效法von Mises)称为“Bernoulli问题”的一个问题,即αnF(m)的值的问题的解。正如第56节所表明的,一个n-节段可说具有性质“m”,当它正好含有m个1时;因此在这个(有穷)节段内1的相对频率当然是m/n。我们现在可定义:α的一个n-节段有性质“△p”当且仅当它的1的相对频率与αF(1)=p的值,即1在序列α中的概率的离散不超过δ;这里δ是我们任意选取的接近于0的任何小的分数(但不同于0)。我们能用下列说法表示这个条件:一个n节段有性质“△p”,当且仅当[ -p]<δ时;换言之,节段具有性质‘△p’。现在Bernoulli定理回答了频率或概率值的问题,在αn序列内这种节段——具有性质△p的节段的值的问题;因此它回答了αnF(△p)值的问题。 -p]<δ时;换言之,节段具有性质‘△p’。现在Bernoulli定理回答了频率或概率值的问题,在αn序列内这种节段——具有性质△p的节段的值的问题;因此它回答了αnF(△p)值的问题。
人们在直观上可以猜测:如果值δ(δ>0)是固定的,如果n增加,那么具有性质△p的这些节段的值,因此αnF(△P)的值,也将增加(并且它的增加将是千篇一律的)。Bernoulli的证明(在任何一本概率计算教科书中都可以找到这种证明)接着下去便是借助二项式公式来评价这种增加。他发现如果n的增加没有极限,αnF(△P)值便逼近最大值1,不管&的固定值有多少。这可用下式来表示。
(1) F(△p)=1
(对任何△p值) F(△p)=1
(对任何△p值)
这个公式从改变毗邻节段序列的第三个二项式公式而来。对于交迭节段的序列,类似的第二个二项式公式用同样的方法直接导附相应的公式。
(2) F’(△p)=1 F’(△p)=1
这个公式对于交迭节段序列以及从它们之中作正态顺序选择是正确的,因此对于具有后效的序列(Smoluchowski曾研究过这些序列)也是正确的。公式(2)本身产生(1),假如所选的序列不交迭,所以自由度为n。(2)可描述为Bernoulli定理的一种变式;而我在这里将要就Bemoulli定理所说的话经过必要的修正(mutatis
mutandis)以适用于这种变式。
Bernoulli定理,即公式(1),可用下面的话表示。让我们称从一随机序列α中选择的长度固定的一个长的有穷节段为一“中等样本”(fair
sample),当且仅当在这个节段内1的概率,即在随机序列内1的概率值与p的离差只有某一小的固定的分数(我们可以自由挑选这个分数)。因此我们可以说,只要我们使这些节段有足够长,偶然碰到一个中等样本的概率如我们所喜欢的那样逼近于1。
在这个表述中,“概率”(或“概率值”)一词出现两次。在这里如何解释或翻译它?在我的频率定义的意义上,这词不得不翻译如下(我将“概率”一词译为频率语言的两种译法用黑体表示):所有足够长的有限节段中绝大多数有“中等样本”;即它们的相对频率与该随机序列频率值p的离差为一任意固定的很小的量;或简言之:频率p近似地实现在几乎所有足够长的节段中。(我们如何达到p值与我们现在的讨论是无关的;比方说它可以是一种假说性估计的结果。)
记住Bernoulli频率αnF(△p)一成不变地随节段的长度n的增加而增加,一成不变地随n的减少而减少,所以,相对频率值在短的节段中实现是比较罕见的,我们也可说:
Bernoulli定理说明,“绝对自由的”或似机遇的序列的短节段经常表现在与p有比较大的离差,因此有比较大的涨落,而较长的节段,在大多数情况下,将表现出随长度的增加与P的离差越来越小。结果,在足够长的节段中大多数离差将变得如我们希望的那样小;换言之,大的离差将变得如我们希望的那样罕见。
因此,如果我们取随机序列的一个十分长的节段,为了通过计算或也许利用其他的经验的和统计的方法,求在它的子序列内的频率,那么在大多数情况下我们将得到如下结果。有一个特征性平均频率,使整个节段中以及几乎所有的长的子序列中,相对频率与这个平均值的离差很小,如果我们挑选的子节段越短,较小的子节段的相对频率与这个平均值的离差就越大和越经常,这个事实,即有穷节段这种可在统计学上得到确定的行为,系指它们的“拟收敛行为”;或系指这样的事实:随机序列在统计学上是稳定的。
因此,Bernoulli定理断言,似机遇序列的节段较小,经常表现为大的涨落,而大节段总表现恒定或收敛;简言之,我们在小节段中发现无序和随机,在大节段中发现有序和恒定。“大数定律”式所指的正是这种行为。
62.Bernoulli定理和概率陈述的解释
我们刚刚看到,用言语表述的Bernoulli定理中“概率”一词出现了两次。
频率理论家在两种情况下根据它的定义翻译这个词没有困难:他能对Bernoulli定理和大数定律提供一个清楚的解释。主观理论的拥护者也能以它的逻辑形式做到这一点吗?
想把“概率”定义为“理性信仰程度”的主观理论家,当他把“……的概率如我们希望的那样逼近1”这些话解释为“……几乎是确定无疑的”时,他前后完全一致,并且有权这样做。但是当他继续说:“……相对频率与它最可几的值p
的离差小于一定量……”,或用Keynes的话说,“事件出现的比例与最可几的比例p的离散小于一定量……”时,他只不过模糊了他的那些困难。这听起来似乎蛮有道理,至少乍一听来是这样。但是如果在这里我们也把“可几的”(有时省略)一词,用主观理论的意义加以翻译,那么整个问题变成这样:“相对频率与理性信仰程度p值的离差小于一定量几乎是确定无疑的,”我认为这是十足的废话。因为相对频率只能与相对频率作比较,只能与相对频率有离差或没有离差。很清楚,在演绎Bernoulli定理之后,把一个不同于演绎之前给予p的意义给予它是不允许的。
因此我们看到主观理论不能用统计学的大数定律来解释Bernoulli定理。统计定律的推导只有在频率理论的框架内才有可能。如果我们从严格的主观理论出发,将永远达不到统计陈述——即使努力填补同Bernoulli定理之间的鸿沟也不能达到。
63.Bernoulli定理和收敛问题
从认识论观点看,我对上述大数定律的演绎是不满意的;因为收敛公理在我们的分析中所起的作用是很不清楚的。
实际上通过把我的研究限于具有频率极限的数学序列已不言而喻地引入了这类公理(参阅第57节)。结果甚至容易使人认为我们的结果——大数定律的推导——是无关紧要的;因为“绝对自由”的序列在统计学上是稳定的这一事实可被认为是它们的收敛所蕴含的,而它们的收敛如果不是不证自明也是不言自明地被假定的。
但是正如von Mises已清楚地表明的那样,这个观点是错误的。因为有些序列满足收敛公理,虽然Bernoulli定理对它们不适用,因为具有频率接近1的任何长度的节段,出现在与p有一定程度离散的频率中。(极限p在这些情况下的存在是由于这个事实:虽然离散可无限增加,但它们相互抵销。)这些序列看起来仿佛它们在任意大的节段中是发散的。即使相应的频率序列事实上是收敛的。因此大数定律根本不是收敛公理的无关紧要的推断,而且,这个公理对于推导大数定律完全不充分。这就是为什么我对随机公理的修改,“绝对自由”的要求是不可缺少的。
然而,我们的理论重建,提示了这样一种可能性:大数定律也许是独立于收敛公理的。因为我们已经看到,Bernoulli定理是直接从二项式公式中得出的;此外,我已证明,可为有穷序列推导出第一个二项式公式,因此当然无需任何收敛公理。还必须假定的一切是参考序列α的自由度至少是n-1;这是一个从中得出特殊乘法定理的可靠性以及第一个二项式公式的可靠性的假定。为了过渡到极限,为了获得Bernoulli定理,只需假定我们使n如我们希望的那样大。因此就能看出,Bernoulli定理大概是对的,即使对于有穷序列也是如此,如果对于一个足够大的n它们的自由度为n的话。
所以看来Bernoulli定理的演绎并不依赖于假定频率极限存在的公理,而是仅依赖于“绝对自由度”或随机性。极限概念仅起次要的作用:它用来把相对频率的概念(在第一个例子中给它下定义只是为了有穷类,没有它,n-自由度的概念就不能提出)应用于能无限延伸的序列。
此外,不应忘记,Bernoulli本人是在经典理论的框架内演绎他的定理的,这个理论不包含收敛公理;也不应忘记,作为频率极限的概率定义只是经典形式体系的一种解释——而且不是惟一可能的一种解释。
我将试图用除n-自由度(应适当地加以定义)外无需假定任何东西就可推演出这个定理来证明我的推测——Bernoulli定理独立于收敛公理。并且我将试图证明它甚至适用于其主要性质并不具有频率极限的那些数学序列。
只要能够证明这一点,我就会认为我之推演出大数定律从认识论家的观点来看是令人满意的。因为似机遇经验序列证明,我已描述为“收敛”或“统计学上稳定的”那种特殊行为,是一个“经验事实”——或至少有时人们这样告诉我们(参阅第61节)。通过用统计方法记录长节段的行为,人们能够确定相对频率越来越逼近一个限定的值,相对频率在其中涨落的间隔变得越来越小。对这种所谓的“经验事实”,已进行过如此多的讨论和分析,确实往往认为它是大数定律的经验验证,对这种“经验事实”可以从不同角度来看。具有归纳主义倾向的思想家大多数认为它是基本的自然律,不能还原为任何更简单的陈述;认为它是必须完全加以接受的我们世界的特性。他们认为以适当形式——例如以收敛公理的形式——表示的这个自然律应该作为概率论的基础,从而使概率论具有一门自然科学的性质。
我对这种所谓“经验事实”的态度是不同的。我倾向于认为,它可还原为序列的似定律性质;可从这些序列的自由度为n的事实中推导出来。我认为Bermoulli和Poisson在概率论领域的成就正是在于他们发现了一种方法以表明这种所谓“经验事实”是重言式,表明从小规模的无序(假如它满足表述得合适的n-自由度条件)合乎逻辑地得出一种大规模的稳定性秩序。
如果我们能够无需假定收敛公理而演绎出Bernoulli定理,那么我们就可把大数定律的认识论问题还原为一个公理独立性问题,因而还原为一个纯粹的逻辑问题。这种演绎也说明为什么收敛公理在各种实际应用(试图计算经验序列的近似行为)中起了很好的作用。因为即使对收敛序列的限制结果弄清是不必要的,利用收敛数学序列来计算经验序列的近似行为(它根据逻辑上的理由在统计学上是稳定的)肯定不是不合适的。
64.收敛公理的排除“机遇理论基本问题”的解决
迄今频率极限除了具有提供一个可应用于无穷序列相对频率的明确概念外,在我们的概率论的重建中没有其他功能,因此我们可以借助它来定义(不受后效约束的)“绝对自由度”。因为正是相对频率被要求不受根据先行者作出选择的影响。
我们早就把我们的研究限制在具有频率极限的二择一,因此不言而喻地引入了收敛公理。现在,为了使我们摆脱这个公理,我将摆脱这个限制,而不用任何其它限制来代替它。这就是说我将不得不建构一个频率概念,它能接管被排除的频率极限的功能,并可应用于所有的无穷参考序列。
满足这些条件的一个频率概念是相对频率序列聚点的概念。(如果在任何给定的元素之后有一些与α的离差小于一定量,即使这个量很小,就说α值是某一序列的聚点。)这个概念可不加限制地应用于所有无穷序列,这一点可从这个事实中看出,即对于每一个有穷的二择一,与之相应的相对频率序列中必有至少一个这样的聚点存在。由于相对频率决不可能大于1,也不可能小于0,相对频率序列必定由1和0连结起来。而且作为一个无穷的连结起来的序列,它必须(根据著名的Bolzano和Weierstrass)至少有一个聚点。
简而言之,与一个二择一α相应的相对频率序列的第一个聚点被称为“α的中频率(midddle frequency)”。因此,我们可以说:如果一个序列α有一个并且只有一个中频率,那么同时这就是它的频率极限;反之亦然:如果它没有频率极限,那么它就有不止一个中频率。
将会发现中频率概念十分适合于我们的目的。正如前面p
是序列α的频率极限这一点是我们的估计——也许是假说性估计——一样,我们现在也可以使用p是α的中频率这一估计。而且假如我们采取必要的预防措施,我们能够借助这些估计的中频率进行计算,类似我们用频率极限计算一样。此外,中频率概念可应用于所有可能的无穷参考序列,没有任何限制。
如果我们现在试图把我们的符号αF’(β)解释为中频率,而不是频率极限,并且我们因而改变客观概率的定义(第59节),我们的公式大多数仍然是可推导的。然而有一个困难:某一中频率不是惟一的。如果我们估计或推测一个中频率是αF’(β)=p
,那么这不排除αF’(β)有除了p以外的值。如果我们假定这并非如此,那就不言而喻要引入收敛公理。如果在另一方面,我们定义客观概率无需这种具有惟一性的假定,那么我们就获得(至少在第一个例子中)一个模棱两可的概率概念;因为在某些条件下一个序列可同时拥有都是“绝对自由的”若干中频率。但是这是难以接受的,因为我们习惯于用不含糊的或惟一的概率;也就是假定在同一参考序列内对于同一性质,可能有一个,并且只可能有一个概率p。
然而,无需极限公理定义惟一的概率概念的困难是容易克服的。我们可引入惟一性要求(毕竟是最自然的程度)作为最后一步,在假定了序列将是“绝对自由的”以后。这使我们对我们的似机遇序列定义以及客观概率定义提出下列修改作为对问题的一种解决办法。
设α为一个二择一(有一个或数个中频率)。设α的1有一个或只有一个“绝对自由的”中频率p;于是我们说α是似机遇或随机的,并且p是1在α内的客观概率。
这有助于把这个定义分为两个公理性要求。
(1)随机性要求:对于似机遇的二择一,至少必须有一个“绝对自由的”中频率,即它的客观概率p。
(2)惟一性要求:对于同一似机遇的二择一的同一性质,必定有一个且只有一个概率p。
前面建构的实例保证了这个新公理系统的无矛盾性。有可能建构不具有频率极限的序列,虽然它们有一个且只有一个概率。这表明新的公理要来实际上比老的更广泛,更不确切。如果我们以下列形式陈述(如我们可以陈述的那样)我们的老公理,这个事实甚至会变得更加明显:
(1)随机性要求:如上。
(2)惟一性要求:如上。
(2’)收敛公理:对于同一似机遇二择一的同一性质除了它的概率p外不存在其他中频率。
我们可从建议的要求系统中演绎出Bernoulli定理,以及同它一起的经典概率计算定理。这就解决了我们的问题:现在有可能在频率理论的框架内演绎出大数定律,而无需利用收敛公理。此外,不仅第61节公式(1)和Bernoulli定理的文字表述仍然不变,而且我们给予它的解释也仍然不变:在一个没有频率极限的似机遇序列情况下,几乎所有足够长的序列表明与p只有小的离差,这仍然是正确的。在这些序列中(正如在有频率极限的似机遇序列一样)具有拟发散行为的任何长度的节段,也就是与p的离差有任何量的节段,当然不时会出现。但是这些节段比较罕见,因为它们必定被其中所有的(或几乎所有的)节段具有拟收敛行为的序列极端长的部分所补偿。正如计算所表明的,这些延伸部分一定会比它们补偿的具有发散行为的节段长几个数量级。
这也就是解决“机遇理论基本问题”(在第49节就是这样称呼的)的地方。从单个事件的不可预测性和不规则性到概率计算规则对这些事件的可应用性,这看起来自相矛盾的推论实际上是可靠的。假如根据这样一个假说性假定,即在根据先行者所作的任何选择中只出现一个循环的频率——“中频率”——因而没有后效发生,我们就能够以相当的逼近度来表示不规则性。因为根据这些假定,有可能证明大数定律是重言的。坚持这样的结论,即在可以说任何事情在这时和那时都会发生的——虽然某些事情的发生只是罕见的——不规则序列中,某种规则性或稳定性将出现在十分大的子序列中,这是可以允许的,并非自相矛盾的(有人有此主张)。这个结论也不是不重要的,因为为了这个结论我们就需要特殊的数学工具(Bolzano和Weierstrass定理,n-自由度概念,以及Bernoulli定理)。当我们知道,不规则性的假定可以置于某种频率假说(不受后效约束的假说)的形式中,并且知道,如果我们要证明从不可预测性到可预测性,从无知到知识的推论的可靠性,它就必须置于这种形式中,那么这种推论外表的自相矛盾就消失了。
现在已变得很清楚,为什么老的理论不可能适当处理我所说的“基本问题”。大家承认,主观理论能够演绎出Bernoulli定理;但是在大数定理时兴以后它决不能用频率前后一致地解释它(参阅第62节)。因此它决不能说明概率预测统计学上的成功,另一方面,老的频率理论,根据它的收敛公理则明确要求有规则性。因此在这个理论内不会有从小规模的不规则性推论到大规模的稳定性问题,因为它只涉及从大规模的稳定性(收敛公理)同小规模的不规则性(随机公理)结合在一起,推论到大规模的特殊形式的和稳定性(Bernoulli定理,大数定律)。
收敛公理不是概率计算基础的一个必要部分。我用这个结果来结束我的数学计算分析。
现在我们回来考虑性质截然不同的方法论问题,尤其是如何判定概率陈述问题。
65.可判定性问题
无论我们可给概率概念下什么定义,或我们选择什么样的公理表述:只要二项式公式在系统内是可推导出来的,概率陈述就是不可证伪的。概率假说并不排除任何可观察的东西;概率陈述不可能同一个基础陈述发生矛盾,或被它反驳;它们也不可能被任何有限数目的基础陈述所反驳;因此也就不会被任何有限数目的观察所反驳。
让我们假定我们已对某个二择一α提出某个均等机遇假说;例如我们已估计到用一块硬币作掷猜出现“1”和“0”的频率是均等的,因此 αF(1)-
αF(0)=1/2;再让我们假定我们在经验上发现无例外地一次又一次出现“1”:于是我们无疑会在实际上放弃我们的估计,认为它已被证伪。但在逻辑的意义上不可能有证伪问题。因为我们可以肯定观察的只是一个有限的掷猜序列。并且虽然根据二项式公式,碰巧出现与1/2的离差很大的十分长的有限节段的频率是极小的,然而它必定总仍然是大于0。因此具有甚至最大离差的有限节段十分罕见的出现决不可能反驳这个估计。实际上,我们必定会期望它出现:这是我们估计的一个推断。任何这种节段可计算的罕见性将是证伪概率估计的一种手段,这种希望证明是要落空的,因为甚至一个长的、离差大的节段的频率出现,也总可以说不过是一个更长、离差更大的节段的一次出现。因此不存在在外延方面给定的事件序列,所以不存在能够证伪概率陈述的有限的几个一组的基础陈述。
只有一个无穷的事件序列——根据某项规则在内包上加以定义的——能反驳一个概率估计。但是鉴于第38节阐述的考虑(参阅第43节),这就是说,概率假说是不可证伪的,因为它们的维(dimension)是无限的。所以我们实际上应把它们描述为经验上没有信息的、没有经验内容的。
然而面对物理学利用从概率假说性估计那里得到的预测所取得的成功,任何这种观点显然是不能接受的。(这里所用的论据同早些时候用来反对主观理论把概率解释为重言的论据是一样的。)许多这些估计的科学意义不亚于其他任何物理学假说(例如,不下于某一决定论性质的假说)。并且物理学家常常很能判定他是否可暂时接受某种特定的概率假说为“经验上得到确证的”,或他是否应该把它作为“实践上被证伪的”而加以摈弃,即对于预测设有用处。十分明显,这种“实践上被证伪”只能通过方法论上的判定才能获得,以把高度不可几的事件认作被排除的——被禁止的。但是根据什么理由可认为它们如此呢?我们应从什么地方获得这种思路?这种“高度不可几性”从哪里开始?
由于从纯逻辑观点看,概率陈述不可能被证伪这个事实是不可能有什么疑问的,我们在经验上使用它们这个同样不容置疑的事实似乎必定是对我关于方法(我的划界标准决定性地依赖于它)的基本思想的致命打击。然而我将通过果敢地应用这些思想来试图回答我已提出的问题——什么是可判定性问题。但是要做到这一点,我将首先不得不分析概率陈述的逻辑形式,既考虑到它们之间逻辑上的相互关系,又考虑到它们与基础陈述所处的逻辑关系。
66.概率陈述的逻辑形式
概率估计不是可证伪的。当然,它们也不是可证实的。同样理由这也适用于其他假说,因为看到任何实验结果,不管多么多和多么有利,最后总能确定“正”的相对频率是1/2,并且将总是1/2。
因此概率陈述和基础陈述不可能相互矛盾,也不可能彼此蕴含。然而由此得出结论说概率陈述和基础陈述之间没有任何逻辑关系,那就错了。并且同样不能认为虽然在这两类陈述之间有逻辑关系(因为观察序列同频率陈述显然或多或少是接近一致的),这些关系的分析迫使我们引入一种突破经典逻辑的特殊概率逻辑。与这些观点相反,我认为这些关系完全能够用可推演性和矛盾的“经典”逻辑关系来分析。
从概率陈述的非可证伪性和非可证实性可以推论出,它们没有可证伪的推断,它们本身不可能是可证实陈述的推断。但是相反的可能性并未排除。因为它可以是(α)它们有单向可证实推断[纯粹存在推断,或有推断(there-is-conse-quences)]或(b)它们本身是单向可证伪全称陈述[所有-
陈述(all—statements)]的推断。
可能性(b)对于弄清概率陈述和基础陈述之间的逻辑关系鲜有帮助:一个非可证伪陈述,即一个说得很少的陈述能够属于可证伪的、因而说得更多的陈述的推断类,这是非常明显的。
对我们意义更大的是可能性(α),它无论如何不是没有意义的,并且事实上结果证明对我们分析概率陈述和基础陈述之间关系是基本的。因为我们发现能够从每一个概率陈述中演绎出无限类的存在陈述,但反之不然。(因此概率陈述断言的比任何这些存在陈述断言的更多。)例如,设p是对某一二择一假说性估计的概率(并设0≠p≠1);那么我们能从这个估计中演绎出例如1和0都将出现在这序列的存在推断。(当然也还有许多远不是那么简单的例子——例如,会出现与p的离差仅为一非常小的量的节段。)
但是我们从这个估计中能演绎出的多得多;例如“一遍又一遍地”出现一个具有性质“1”的元素和具有性质“0’的另一个元素;那就是说,在任何元素x之后,在序列中会出现一个具有性质“1”的元素y,并且也出现一个具有性质“0”的元素x。这种形式的陈述(“对于每一个x有y具有可观察的、或外延上可检验的性质B”)既是不可证伪的——因为它没有可证伪的推断——又是不可证实的——由于使之成为假说性的“所有”或“对于每一个”。虽然如此,它能够得到更好地或不那么好地“确证”——指我们可以证实它的许多或很少存在推断,或者不能证实它的存在推断;因此它与基础陈述处于似是概率陈述特有的关系中。上述形式的陈述可称为“全称化的存在陈述”或(全称化的)“存在假说”。
我的主张是,概率估计对基础陈述的关系,以及这些估计或多或少得到很好“确证”的可能性,考虑到这一事实就能理解:存在假说在逻辑上可从所有概率估计中演绎出来。这对概率陈述本身是否可有存在假说的问题是有启发的。
一切(假说性的)概率估计蕴含着这样的推测:所说的经验序列几乎是似机遇和随机的。这就是说,它蕴含着概率计算公理的(近似的)可应用性,以及真理性。所以,我们的问题就是这些公理是否代表我所说的“存在假说”的问题。
如果我们检查一下第64节中提出的两个要求,那么我们发现随机性要求实际上具有存在假说的形式。另一方面,惟一性要求则没有这种形式;它不可能有这种形式,因为这种形式的陈述“只有一个……(There
is only one……)”必然具有全称陈述的形式。(可译为“至多一个……”或“所有……是同一的”。)
在这里我的论点是,正是概率估计的(可称之为的)“存在成份”,因而正是随机性的要求,概率估计和基础陈述之间才建立起一种逻辑关系。因此,惟一性的要求,作为全称陈述,没有任何外延的推断(extensional
consequences)。具有所要求性质的p的值存在这一点确定能够在外延上得到“确证”——虽然只是暂时地;但是只存在一个这样的值这一点则不能。这后一个全称的陈述可能在外延上有意义,仅当基础陈述能够同它发生矛盾时;这就是说,仅当基础陈述能够肯定存在的值不止这一个时。由于它们不能够(因为我们记得不可证伪性与二项式有密切关系)做到这一点,惟一性的要求必然在外延上是没有意义的。
这就是为什么如果我们从系统中消去惟一性要求,概率估计和基础陈述以及前者的分级“可确证性”之的分级之间所有的逻辑关系不受影响的缘故。在这样做时,我们能够给予系统以纯粹存在假说的形式。但是我们因此不得不放弃概率估计的惟一性,并且因而(就惟一性而言)获得某种不同于通常概率计算的东西。
所以惟一性的要求显然不是多余的。那么它的逻辑功能是什么?
虽然随机性要求有助于确立概率陈述和基础陈述之间的某种关系,惟一性要求调节着各种概率陈述本身之间的关系。没有惟一性要求,作为存在假说的某些陈述,可以从其他陈述中推导出来,但是它们决不可能彼此矛盾。只有惟一性的要求才保证,概率陈述能彼此矛盾;因为根据这个要求它们获得其成分为一个全称陈述和一个存在假说的合取形式;并且这种形式的陈述能够彼此处于同样基本的逻辑关系中(同义、可推导性、相容性和不相容性),正如任何理论——例如一个可证伪的理论——的“正常的”全称陈述那样。
如果我们现在考虑收敛公理,那么我们发现,在它具有一种不可证伪的全称陈述的形式这一点上它类似惟一性要求。但是收敛公理要求的比惟一性要求的更多。然而这种附加要求也不可能有任何外延上的意义;此外,它没有逻辑或形式的意义,而只有内包上的意义:它要求排除所有没有频率极限的用内包定义的(即数学的)序列。但是从应用观点看,这种排除证明甚至在内包上也没有意义,因为在应用概率论中我们当然不涉及数学序列本身,而只涉及经验序列的假说性估计。所以排除没有频率极限的序列,只能用来告诫我们不要把那些经验序列着作为似机遇或随机的,对于那些经验序列我们假定它们没有频率极限。但是对这种告诫,我们能够采取何种可能的行动?鉴于这种告诫,我们应该容许或避免哪类关于经验序列可能收敛或发散的考虑或推测,保证收敛标准同发散标准一样可应用于这些序列?一旦摆脱了收敛公理,所有这些尴尬的问题也就消失了。
因此我们的逻辑分析使系统各部分的要求的形式和功能都一目了然,并且表明反对随机性公理和支持惟一性要求的理由是什么。同时可判定性问题似乎变得越来越重要。并且虽然我们不一定称我们的要求(或公理)“无意义”,看来我们被迫把它们描述为非经验的。但是概率陈述的这种描述——不管我们用什么话来表达它——是否同我们研究的主要思想相矛盾呢?
67.思辨形而上学的概率系统
概率陈述在物理学中最重要的用处是这样:某些物理学规律性或可观察的物理效应被解释为“宏观定律”;也就是说,它们被解释或说明为大数现象,或假说性的、不能直接观察的“微观事件”的可观察结果。宏观定律用下列方法从概率估计中演绎出来:我们证明,与所说的观察到的规律性一致的观察结果,应该期望其概率十分接近于1,即其概率与1的离差为一个能达到按我们选取的那样小的量。当我们已证明这一点时,那么我们就说,我们已经用我们的概率估计把所说的可观察效应“解释”为一个宏观效应。
但是如果我们以这种方法使用概率估计来“解释”可观察的规律性而不采取特定的预防措施,那么我们会马上陷入某些思辨,根据一般的用法,完全可以把它们描述为思辨形而上学的典型。
因为概率陈述是不可证伪的,以这种方法用概率估计“解释”我们喜欢的任何规律性必定总是可能的。以万有引力定律为例。我们可以下列方法设想出一些假说性的概率估计来“解释”这个定律。我们选择某类事件作为基本事件或原子事件;例如某一小粒子的运动。我们也选择某方面作为这些事件的主要性质;例如粒子运动的方向和速度。于是我们假定这些事件显现出似机遇的分布。最后我们计算出所有的粒子在某一有限的空间区域内,在某一有限的时期内——某一“宇宙期”——将以规定的精确性(附带地说,以万有引力定律要求的方式)运动的概率。计算出的概率当然将十分小;实际上小得微不足道,但是仍然不等于零。因此我们可以提出这样的问题:这个序列的某个n-节段得有多长,或换言之,整个过程必须假定有多长,我们才可期望这种宇宙期出现的概率接近1(或与1的离差不超过某一任意小的值E),在这宇宙期内,作为偶发事件积累的结果,我们的观察将会完全与万有引力定律一致。对于任我们选取的接近于1的任何值,我们获得一个确定的、虽然极端大的有限数。于是我们可以说:如果我们假定序列的节段有这十分大的长度——或换言之,“世界”延续得足够长——那么我们的随机性假定使我们能够期望出现一个方有引力定律似乎也适用的宇宙期,虽然“实际上”除了随机发散外什么也没有出现。借助某种随机性假定,这类“解释”可应用于我们选取的任何规律性。事实上,我们可用这个方式把我们整个世界,以及它的所有被观察到的规律性,“解释”成随机混沌中的一个阶段——纯粹偶然巧合的一种积累。
我认为很清楚,这类思辨是“形而上学的”,它们对科学没有任何意义。并且同样清楚的是:这个事实同它们的不可证伪性——我们能在任何时候和任何条件容许它们这个事实是有联系的。因此我的划界标准似乎同“形而上学的”一词的一般用法是完全一致的。
所以涉及概率的理论,如果它们不加特定预防措施而加以应用,就不应被认为是科学的。如果它们应在经验科学的实践中有用处,我们就必须排除它们的形而上学用法。
68.物理学中的概率
可判定性困难的问题只是方法论的,不是物理学的。如果要求提出一个实践上可应用的概率概念,物理学家也许会提供某种物理学的概率定义,其思路如下:有些实验,即使在受控条件下进行也得出不同的结果。在某些这类实验——“似机遇的”实验,例如用硬币做掷猜——的情况下,经常重复导致具有相对频率的结果,进一步重复,这些相对频率越来越逼近某个固定值,我们可称之为所说事件的概率。这个值是“……可用经验通过一长系列实验确定到任何逼近度”;顺便说,这说明为什么证伪一个假说性的概率估计是可能的。
数学家和逻辑学家会对根据这些思路下的定义提出异议,尤其是下列异议:
(1)这个定义与概率计算并不一致,因为根据Bernoulli定理,只有几乎所有非常长的节段才是统计学上稳定的,即其行为仿佛是收敛的。由于这个理由,概率不能用这稳定性,即用拟收敛行为来定义。因为“几乎所有”一词——它应该出现在定义中——本身只是“十分可几的”一个同义语。因此这定义是循环的;这个事实容易通过去掉“几乎”一词隐避起来(但不能取消)。这就是物理学家的定义所做的事;所以这是不能接受的。
(2)什么时候应说一系列实验是“长的”?不提供一个应称之为“长的”标准,我们不能知道我们何时,或是否已达到逼近这个概率。
(3)我们如何能知道所需要的逼近实际上已达到?
虽然我认为这些异议是合理的,然而我认为我们能够保留物理学家的定义。我将通过上节概述的论据来支持这种见解。这些论据表明当概率假说被允许无限应用时,它们就失去所有信息内容。物理学家决不会以这种方式使用它们。我将遵循物理学家的范例,不允许概率假说的无限应用:我建议我们作为方法论的决定决不把物理效应,即可复制的规律性,解释为偶发事件的累积。这个决定自然修改了概率概念:它使这个概念变窄了。因此异议(1)并不影响我的观点,因为我根本不主张概率的物理概念和数学概念是同一的;反之,我否认这种同一性。但是代替(1),出现了一个新的异议。
(1’)什么时候我们能谈到“累积的偶发事件”?大概在概率很小的情况下。但是什么时候一个概率“小”?我们可以承认的是,我刚提出的建议排除了使用通过改变数学问题的提法,从小概率中制造任意大概率的方法(前节已讨论)。但是为了执行所建议的决定,我们得知道我们应把什么看作是小的。
下面几页将表明所建议的方法论规则与物理学家的定义是一致的,问题(1’)、(2)和(3)提出的异议能借助它得到解答。开始,我脑子里只有一个典型的概率计算应用例子:我脑子里有一些可复制的宏观效应例子,这些效应能够借助精确的(宏观)定律——如气体压力——加以描述,并且我们把这些效应解释或说明为由于微观过程,如分子碰撞大量积累所致。其他典型例子(如统计涨落或似机遇的个别过程的统计)可没有很多困难地还原为这个例子。
让我以这种类型的宏观效应为例,该效应由一个得到很好确认的定律来描述,这个定律可还原为微观事件的随机序列。设这个定律断言在某种条件下某物理量为p值。我们假定效应是“精确的”,因此没有可测量的涨落发生,即与p的离差不超过间距±o(不精确性的间距;参阅第37节),在此间距内我们的测量由于现行测量技术固有的不精确性,无论如何会有涨落。现在我们提出假说:p是微观事件序列α内的概率;其次,n个微观事件促使产生效应。于是(参阅第61节)我们能够对每一个选取的δ值,计算出概率αnF(△P),即测定值将落在间距△P内的概率。补概率可用“E“来表示。因此我们有αnF(△ )=ε。根据Bernoulli定理,随n增加至无限,ε趋向零。 )=ε。根据Bernoulli定理,随n增加至无限,ε趋向零。
我们假定ε“小”到可以不计(在这个假定中有“小”是什么意思的问题(1’),马上就要讨论它)。显然,△p应解释为间距,测量在此间距内逼近p值。由此我们看到三个量:ε,n,和△p与三个问题(1’),(2)和(3)相应。△p或ε可任意选取,它限制了我们选取ε和n的任意性。由于我们的任务是演绎出确切的宏观效应p(±φ),我们不去假定δ大于φ。就可复制效应p而言,如果我们进行的演绎满足δ≤φ
,它就是令人满意的。(这里φ是给定的,由于它是由测量技术来确定的。)现在让我们选取δ使它(近似地)等于φ。于是我们就将问题(3)还原为两个其他问题(1’)和(2)。
通过选取δ(即△P)我们已在n和ε之间确立了一种关系,因为对于每一个n,现在都有一个ε值惟一地与之相应。因此(2),即什么时候n有足够长这个问题已还原为(1’),即什么时候ε小这个问题(反之亦然)。
但是这意味着只要我们能够判定ε的哪一个特定的值可被认为“小到微不足道”而不计,所有三个问题都可得到回答。现在我们的方法论规则等于是决定忽略不计小的ε值;但是我们不准备老是去讨论某个确定的ε值。
如果我们把问题交给物理学家,即如果我们问他,他准备不计什么样的ε——0.001或是0.000001,或是……?他大概会回答E根本不使他感到兴趣;他选取的不是ε而是n;他已这样选取n,使n与△P之间的相关大大独立于我们愿意造成的ε值的任何变化。
由于Bernoulli分布的数学特点,物理学家的回答是有道理的:对每一个n,确定ε和△p之间的函数关系是可能的。对这个函数作一检查就可表明,对于一切(“大的”)n都存在一个表示特征的△p值,使得在这个值的邻域,完全不受ε的变化的影响。这种无影响性随n的增加而增加。如果我们取我们在极端大数现象情况下应该期望的一个数量级的n,那么在它的特征值的领域△p完全不受ε的变化的影响,以致即使ε的数量级改变,△p也几乎根本没有变化。现在物理学家将把很小的值附加于规定得更明确的△p界限上。并且在研究所限的典型的大数现象的情况下,我们记得,能够使△p与精确度为±φ(取决于我们的测量技术)的间距相对应;并且这个间距没有明确的界限,只有我在第37节所说的“缩聚界限”(condensation
bound)。所以当△p在它的特征值(我们能够确定这个值)的领域的无影响性至少有如此之大,甚至ε数量级的改变引起的△p值仅在±φ的缩聚界限内涨落时,我们才称n是大的。(如果n→∞,则△P变得完全不受影响)。但是如果是如此,我们就无需再操心ε的精确测定:即使我们没有精确地说出必须把什么看作是“小的”,决定置小的ε于不顾也就够了。这等于是决定利用上述不受ε的变化的影响的△p的特征值。
必须把极度不可几性置于不顾的规则(只有根据上述才成为十分明确的一条规则)与要求科学的客观性是一致的。因为对我们的规则的明显反对显然是,最大的不可几性始终是一种概率,不管这种概率有多么小,因此甚至最不可几的过程——即我们建议置之不顾的过程——终有一天会发生。但是这个反对意见可通过恢复可复制的物理效应概念来予以解决,这个概念与客观性概念有密切联系(参阅第8节)。我不否认不可几事件会发生的可能性。例如我并不断言在小量气体中的分子在一短暂时间内不会自发地聚集成为这容量的一部分,或者在大量气体中压力的自发涨落永远不会发生。我断言的是,这些偶发事件不是物理效应,因为根据它们的极度不可几性,它们不能随意复制。即使一个物理学家碰巧观察到这种过程,他也完全不可能去复制它,因此永远不能判定在这种情况下实际发生了什么,他是否有可能犯了一次观察上的错误。然而,如果我们发现一些可复制的离差,这些离差不同于按上述方式从概率估计中演绎出的宏观效应,那么我们必须假定概率估计已被证伪。
这些考虑可帮助我们理解Eddington的下述看法,他区别了两类物理定律:“某些事情永远不会在物理世界中发生,因为它们是不可能的;另一些则因为它们也是不可几的。禁止前者的定律是一级定律;禁止后者的是二级定律”。虽然这种表述也许并不能摆脱批评(我宁愿不去对极度不可几的事情是否发生作出不可检验的断言),但它与物理学家对概率论的应用完全一致。
可应用概率论的其他场合,如统计涨落,或似机遇个别事件的统计,可还原为我们一直在讨论的场合,即可精确测定的宏观效应场合。我理解的统计涨落就是Brown运动那样的现象。在这里测量精确度的间距(±o)小于对效应起促进作用的微观事件数n特有的间距△p;因而可期望不同于p的可测定离差是高度不可几的。发生这些离差这一事实是可检验的,因为涨落本身成为一种可复制效应;并且我以前的论证可应用于这种效应:涨落超过某一大小(超过某个间距△p),根据我的方法论要求,必定不是可复制的,朝同一方向涨落的长序列也是如此,如此等等。相应的论证也会适用于似机遇个别事件的统计。
我现在总结我的关于可判定性问题的论证。
我们的问题:概率假说——我们已看到它们是不可证伪的——如何能在经验科学中起自然律的作用?我们的回答是:概率陈述,就它们是不可证伪的而言,是形而上学的和没有经验意义的;就利用它们作为经验陈述而言,利用它们作可证伪的陈述。
但是这种回答提出了另一个问题:概率陈述——是不可证伪的——可用作可证伪陈述,怎么可能呢?(它们能如此使用这个事实是毋庸置疑的:物理学家知道得十分清楚,什么时候认为概率假定已被证伪。)我们发现这个问题有两个方面。一方面,我们必须根据其逻辑形式使利用概率陈述的可能性成为可理解的,另一方面,我们必须分析支配它们用作可证伪陈述的原则。
根据第66节,公认的基础陈述可以多少令人满意地与某种所提出的概率估计一致;它们可更好或稍差一些代表概率序列的一个典型节段。这为某种方法论规则的应用提供了机会,例如要求基础陈述和概率估计之间的一致应该符合某种最低限度标准这一规则。因此规则可引出某种任意的思路,并且规定只有适当代表性的节段(或适当“公平的样本”)才得以“允许”,而不典型的或没有代表性的节段是被禁止的。
对这种意见作更仔细的分析向我们表明,什么被允许和什么被禁止之间的分界线的划定并不一定像起初想象的那样任意。尤其是无需“宽容地”划定这条分界线。因为有可能用这种方式形成这条规则,使什么被允许和什么被禁止之间的分界线,正如其他定律的情况一样,由我们的测量能达到的精确度来决定。
我们根据划界标准提出的方法论规则,不禁止不典型节段的出现;它也不禁止离差(当然,对于概率序列是不典型的)的重复出现。这条规则禁止的是系统离差的出现可预测和可复制,例如朝特定方向的离差,或肯定是不典型的节段的出现。因此它要求的不单是粗略的一致,而是对于可复制和可检验的一切,简言之,对于所有的可复制效应可能是最佳的一致。
69.定律和机遇
人们有时听说,行星的运动服从严格的定律,而一粒骰子的掷下是碰运气,或受机遇支配。我认为区别在于这个事实:迄今我们已能成功地预测行星的运动,但还不能预测掷骰子的个别结果。
为了演绎出预见,人们需要定律和初始条件;如果没有合适的定律或不能确定初始条件,科学的预见方法就垮台。掷骰子时我们所缺乏的显然是初始条件的充分知识。有了初始条件的足够精确的测定,也就有可能在这种情况下作出预见;但是选定正确掷骰子的规则(摇摇骰子盒)是为了防止我们测量初始条件。游戏规则以及确定某一随机序列的各种事件必将发生的那些条件的其他规则,我称之为“框架条件”。它们由这样一些要求组成,如骰子应该是“纯的”(由同质物质组成),应该把它们好好地摇摇等等。
有一些其他情况,预见是不成功的。也许迄今还不可能提出合适的定律;也许发现一个定律的所有尝试都已失败,并且所有的预见也被证伪。在这些情况下我们可能对究竟是否会找到一个满意的定律已失望。(但是大概我们不会放弃尝试,除非问题已使我们不大感兴趣——例如如果我们满足于频率预测,就是这种情况。)然而,无论如何,我们不能定论地说,在某个特定的领域没有定律。(这是证实不可能性的一个结果。)这就是说,我的观点使机遇概念成为主观的。当我们的知识不足以作出预见时我就说“机遇”;正如掷骰子时,我们说“机遇”,因为我们对初始条件没有知识。(可以设想,仪器设备精良的物理学家,能观测其他人预测不到的一次掷骰子的结果。)
与这种主观观点相反,人们有时支持一种客观的观点。就这种观点利用事件本身是指决定的还是不决定的这种形而上学观念而言,我将不在这里对这种观点作进一步的考察(参阅第71和78节)。如果我们的预见获得成功,我们可以谈到“定律”;否则我们对定律或不规则性的存在或不存在不可能有任何知识。
也许比这个形而上学观念更值得考虑的是下面的观点。可以说,当我们的概率估计得到验证时,我们遇到客观意义上的“机遇”;正如当我们遇到因果规律性时一样。
蕴涵在这观点中的机遇定义可能不全是无用的,但是应该有力强调,如此定义的概念并不与定律概念相对立:正是由于这个理由我称概念序列是似机遇的。一般地说,一个实验结果的序列是似机遇的,如果定义序列的框架条件不同于初始条件的话;当在同一框架条件下进行的个别实验,在不同的初始条件下进行时,就会产生不同的结果。其元素根本不可预测的似机遇序列是否存在,我不知道。我们甚至不能从某个序列是似机遇的这个事实,推论出它的元素是不可预测的,还是或者推论出它们“由于”在主观的知识不足意义上的“机遇”所致;我们尤其不能从这个事实推论出定律不存在的“客观”事实。
不仅不可能从序列的似机遇性质中推论出任何与定律一致的东西,或者在另一方面与个别事件一致的东西;甚至不可能从概率估计的验证推论出序列本身是完全不规则的。因为我们知道似机遇序列是存在的,这些序列是根据数学规则建构的。一个序列具有Bernoulli分布这个事实不是不存在定律的征候,与“根据定义”不存在定律完全不是一回事。我们在概率预测成功中看到的不过是在序列结构中不存在简单定律的征候(参阅第43和48节)——与构成序列的事件相反。不受后效约束的假定相当于这样的假说:这种简单的定律是不可发现的,这个假定得到验证,但这就是一切。
70.从微观定律推演宏观定律的可能性
有一种学说几乎已成为偏见,虽然它在最近已受到严厉的批评——所有可观察的事件必须解释为宏观事件,即解释为一些微观事件的平均数或累计或总和的学说(这个学说有点类似某些形式的唯物主义)。像其他这种学说一样,这似是某一方法论规则的形而上学具体化,而这条规则本身是完全无可非议的。我指的是这条规则:我们应该看看我们是否能用上述类型的解释性假说简化、概括或统一我们的理论。在评论这些尝试的成功时,认为关于微观事件的非统计假说及其相互作用定律就能足以说明宏观事件,这是个错误。除此以外,我们应该需要假说性的频率估计,因为从统计前提中只能推导出统计结论。这些频率估计总是独立的假说,当我们从事研究与微观事件有关的定律时,这些假说的确不时出现在我们脑中,但是它们决不能从这些定律中推导出来。频率估计形成一类特殊的假说:一般地说,它们是与规律性有关的禁律。Von
Mises对这一点说得十分清楚:“没有统计学性质的补充假定,在气体动力理论中甚至最微不足道的定理也不是单从经典物理学中推导出来的”。
统计学估计或频率陈述决不能从“决定论”性质的定律中推导出来,理由是为了从这些定律中演绎出任何预见,需要初始条件。在初始条件那里,关于初始条件统计学分布的假定——也就是说特定的统计学假定——进入了演绎过程,统计学定律就是通过演绎从决定论性质或“精确”性质的微观假定中获得的。
理论物理学的频率假定在一定程度上是等机遇假说,这是一个令人惊异的事实,但这无论如何并不是意味着它们是“自明的”,或先验地正确的。它们远非如此,这一点从经典统计学、Bose-Einstein统计学和Fermi-Dirac统计学之间的广泛差异中就可看到。这些表明特定的假定如何可与一个等机遇的假说结合起来,在每一种情况下都导致参考序列的主要性质(假定其分布是均等的)的不同定义。
下面的例子也许可证明这个事实:甚至当我们想摆脱频率假定时,它们也是必不可少的。
想象一个瀑布。我们可辨认某种奇特的规律性:组成瀑布的水流的大小是变化的;不时地飞溅从主流中甩出来;然而在贯穿所有这些变化中,某种规律性明显可见,它强烈提示有一种统计学效应。尽管有一些尚未解诀的液体动力学问题(与涡流的形成有关等等),我们在原则上能够以任何所需程度的精确性,预测任何量水——比方说一组分子——的路线,如果给定足够精确的初始条件的话。因此我们可以假定,有可能预言远在瀑布之上的任何分子,在哪一点上它将越过边缘,到达底部等等。这样原则上可计算出任何数量分子的路线;并且给定充分的初始条件,我们就能在原则上演绎出瀑布的任何一种个别的统计学涨落。但是只能是这种或那种个别的涨落的,而不是我们已描述过的反复发生的统计学规律性,一般统计学分布就更不行了。为了说明这些,我们需要统计学估计——至少假定某些初始条件对于许多不同组的粒子(等于一个全称陈述)将一次又一次地反复出现。我们获得一个统计结果,当且仅当我们作出这些特定的统计学假定——例如关于反复出现的初始条件频率分布的假定——时。
71.形式上单称的概率陈述
我称一个概率陈述为“形式上单称的”,当它把某一概率赋予某个单一偶发事件或某类偶发事件的单个元素时;例如,“用这个骰子掷下一次得5的概率是1/6”或“(用这个骰子)掷任何一次得5的概率是1/6”。从频率理论观点看,一般认为这些陈述是不十分正确的表述,因为不能把概率归之于单个偶发事件,而只能归之于偶发事件或事件有限序列。然而借助客观概率或相对频率概念用适当定义的形式上单称的概率把这些陈述解释为正确的陈述是容易的。我用“Pαk(β)”表示这形式上单称的概率:作为序列α的一个元素,某一偶发事件k有性质β——符号为kεα——于是我定义形式上单称的概率如下;
Pαk(β)=αF(β)(kεα)(定义)
这可用文字表达如下:事件k具有性质β——设k为序列α的一个元素——的形式上单称的概率,根据定义等于性质β在参考序列α内的概率。
这个简单的几乎一目了然的定义证明令人惊异地有用。它甚至可帮助我们澄清现代量予理论的某些复杂问题(参阅第75-76节)。
正如定义所表明的,如果一个形式上单称的概率陈述没有明确说出一个参考类,它就是不完全的。但是虽然α常常没有明确提及,在这些情况下我们往往知道α是什么意思,因此上述第一个例子没有具体规定任何参考序列α,但是十分清楚它与掷真的骰子的所有序列有关。
在许多情况下,对一个事件K可以有若干不同的参考序列。在这些情况下非常明显,对同一事件可以作出不同的形式上单称的概率陈述。因此一个个别的人K将在一定时期内死亡这种概率可根据我们认为他是他的年龄组的一员,还是他的职业组的一员等等来假定十分不同的值。对于应该从若干可能的参考类中选定哪一个,不可能制定一个一般规则。(最窄的参考类往往最合适,假如它多到足以使概率陈述立足于合理的统计外推,并且得到足够量验证证据的支持的话。)
一旦我们认识到同一偶发事件或事件可以有不同的概率,作为不同参考类的一个元素,不少所谓概率悖论就消失了。例如,有时有人说,一个事件的概率αPk(β)在它出现以前不同于同一事件在它出现以后的概率:在以前它等于1/6,而在以后可能只等于1或0。当然这个观点是完全错误的。αPk(β)在出现以前和以后总是相同的。除了根据信息kεβ(或kε )——根据时偶发事件的观察提供给我们的信息——我们可选取一个新的参考类,即β(或 )——根据时偶发事件的观察提供给我们的信息——我们可选取一个新的参考类,即β(或 ),然后向βPk(β)值是什么以外,什么也没有变化。这个概率值当然是1;而 ),然后向βPk(β)值是什么以外,什么也没有变化。这个概率值当然是1;而 Pk(β)=0。告诉给我们关于单个偶发事件实际结局的陈述——不是关于某个频率,而是关于“kεφ”形式的陈述——不能改变这些偶发事件的概率;然而,它们可提示我们选取另一个参考类。 Pk(β)=0。告诉给我们关于单个偶发事件实际结局的陈述——不是关于某个频率,而是关于“kεφ”形式的陈述——不能改变这些偶发事件的概率;然而,它们可提示我们选取另一个参考类。
形式上单称的概率陈述概念提供了一种通向主观理论,从而也就通向域(range)理论的桥梁,正如下节将表明的那样。因为我们会同意把形式上全称的概率解释为“理性信仰程度”(依照Keynes)——假如我们允许我们的“理性信仰”受某一客观的频率陈述指导的话。因此这种陈述还是我们的信仰所依靠的信息。换言之,也可能有这样的事:我们除了知道某个事件属于某一参考类,某个概率估计在其中受到了成功的检验外,对它一无所知。这个信息并不能使我们预见这个事件的性质将是什么;但是它能使我们表达借助某种形式上单称的概率陈述知道它的一切,这种陈述看起来像关于所谈论的特定事件的不确定预见。
因此,我不反对关于单个事件概率陈述的主观解释,即解释为不确定的预见——可以说,承认我们对所谈论的特定事件缺乏知识(的确,关于这个事件什么结论也不能从某个频率陈述中得出)。那就是说,我不反对概率陈述的主观解释,只要我们明确承认客观频率陈述是基本的,因为只有它们是可用经验检验的。然而,我反对把这些形式上单称的概率陈述——这些不确定预见——解释为关于客观事态的陈述,但不反对解释为客观统计事态的陈述。我脑子里有这样一种观点:关于掷骰子概率为1/6的一个陈述不仅是承认我们不知道任何确定的事情(主观理论),而且是关于掷下一次的断言——断言它的结果客观上既是不确定的又是非决定的——是关于某种仍悬而未决的事情的断言。我认为所有作出这种客观解释(除了别人外,Jeans作过充分的讨论)的尝试都是错误的。不管这些解释可能造成一些什么样的非决定论气氛,它们全都包含这样的形而上学思想:不仅我们能演绎出和检验预见,并且除此之外自然界或多或少是“决定的”(或“非决定的”);因此预见的成败不应用它们由之演绎出来的定律来解释,而是首先由这样一个事实来解释:自然界实际上是(或不是)根据这些定律组成的。
72.域理论
我在第34节中说,一个可证伪程度比另一陈述更高的陈述可被描述为逻辑上更不可几的陈述;而不那么可证协的陈述则是逻辑上更可几的陈述。逻辑上不那么可几的陈述衍推出逻辑上更可几的陈述。在逻辑概率概念和客观的或形式上单称的数值概率概念之间有密切关系。某些概率哲学家(Bolzano,von
Kries,Waismann)曾试图把概率计算立足于逻辑域,因此立足于一个与逻辑概率一致的概念(参阅第37节);并且他们在这样做时,也试图弄清逻辑概率与数值概率之间的密切关系。
Waismann曾建议用与不同陈述相应的相对频率测定它们逻辑域之间的相互关系程度(可以说它们的比值),从而把频率看作为决定一个测定域的系统的东西。我认为在此基础上建立概率论是可行的。的确我们可以说,这个计划就是使相对频率同某些“不确定的预见”相关起来——正如当我们定义形式上的单称概率陈述时在前一节已经做的一样。
然而必须说,仅当一个频率理论已经建构时,这种定义概率的方法才是可行的。否则人们就得问在定义测定系统时使用的频率本身又是如何定义的。然而,如果我们手中已经有某个频率理论,那么引入域理论实际上就成为多余的。但是尽管有这种异议,我认为Waismann建议的可行性是重要的。发现一个更全面的理论能够填补解决这个问题的各种尝试之间,尤其是在主观和客观解释之间的鸿沟——起初似乎是不可填补的。然而Waismann的建议要求作一点修改。他的域比值概念(参阅第48节注)不仅要求域能借助它们的子类关系(或它们的衍推关系)加以比较;而且它更一般地要求使甚至只是部分交迭的域(不可比较的陈述的域)也能够成为可以比较的。然而这后一个假定有相当的困难,它是多余的。有可能表明,在有关的情况下(为随机情况)子类的比较和频率的比较必定导致类似的结果。这证明为了测定域而把频率与域相关起来的方法是对的。我们在这样做时,就使所谈论的陈述(按子类方法是不可比较的)成为可以比较的。我将粗略地表明所描述的方法如何可得到证明。
如果在两个性质类γ和β之间,子类关系γ B成立,则: B成立,则:
(K)〔Fsb(kεγ)≥Fsb(kεβ)〕(参阅第33节)
因此逻辑概率或陈述(kεγ)的域必须小于或等于(kεβ)的域。它将是相等的,仅当有一个参考类α(它可以是全称类)时,对于这个参考类下列规则成立,这个规则可以说具有“自然律”的形式:
(x){[xε(α.β)→(xεγ)]}
α.β
如果这种“自然律”不成立,因此我们可假定在这个方面有随机性,那么不等性就成立。但是在这个情况下我们就得到下式,假如α是可数的,并可承认为一个参考序列:
αF(γ)<αF(β)
这就是说,在随意性情况下,域的比较必须导致同样的不等性,正如相对频率的比较一样。因此,如果我们有随机性,我们就可把相对频率同域相关起来,以使域成为可测量的。但是这正是我们在第71节中当我们定义形式上单称的概率陈述时所做的(虽然是间接地)。的确,我们可以从这些假定中直接推论出
αPk(γ)<αPk(β)
这样我们就回到了我们的出发点,概率解释问题。并且我们现在发现,客观和主观理论之间的冲突,初看似乎是如此难办,可用某种一目了然的形式上单称的概率的定义来完全消除。 |