|
只要经济学家们认真对待边际效用递减这一直觉概念,他们就不可能通过效用最大化理论简单扩展而对所观察到的、与涉及不确定性的选择有关的行为加以合理的说明。这一点可以直接通过下面的例子加以说明。设想一次赌博,每人都有50%的机会获得或失掉100美元。这一赌博的数学期望值为0。既然增添的100美元在效用上的所得小于失去100美元在效用上的损失。因此,如果货币边际效用被认为是递减的,则这一赌博的精神期望,也就是作为接受这一赌博的结果在效用上的预期变化,就小于0或为负值,接受这种赌博暗示着一次效用上的损失;因而,马歇尔和其他人得出结论认为赌博是“非理性的”。像赌博这样的活动被认为无法以效用最大化为根据来解释。然而,如果我们不考虑边际效用递减的假设,就会出现这样的情况,我们可以像分析其他选择那样,利用相同的效用最大值假设来分析涉及到不确定性的选择。
一旦引入了不确定性,选择的目标就不再是由已知成份组成的一组货物,而是一组直相排斥的选择,每种选择都有某种特定的概率值。我们可以把一笔钱——或一笔收入——看成表示一种概率(既然这种收入在不同货物中的最优配置已由确定性条件下的选择理论进行了讨论),因此,一个选择的目标将是收入的一种概率分布;例如,获得收入I1的概率P1,获得收入I2的概率P2,获得收入I3的P3,等等,各概率之和为一。选择的另一个目标将是一种不同的概率分布。我们现在可以把建立用以合理地说明在这些目标之间进行选择的理论作为我们的课题。
预期效用最大化
让B表示这类选择的一般化目标,也就是表示一组或“一揽子”可供选择的收入及其相应的概率(如果我们要对不同组进行对比,我们将使用下角标志,也就是B1表示一组,B2表示另一组,等等)。我们将假设,个人能够排列这些选择目标,而这些排列服从传递条件,因而如果他把B1排列在B2之上,把B2排列在B3之上,他会把B1
排列在B3之上。让函数G(B)表示这一排列,也就是G(B)是一个函数,它对于每个目标或每笔款项(每个B)赋予一个数字,而且这些数字具有个人会优先选择一个有较高数字的B,而不是有着较低数字的B的性质,也就是说,这些数字根据这个人的偏好,表示出所有款项的一种排列。为了与确定性条件下的选择理论所用的语言相一致,G(B)可以看作是给出了与各种收入的概率分布相对应的“效用”。
直到目前为止,所表述的理论几乎完全是一般性的,因此,也几乎完全是空洞的。它仅仅是讲,个人对各种互相替代的可能性进行排列并在他们可以选择的那些替代办法中选择他们列为最高的一个。它的唯一内容在于假设各种选择的一致性和传递性。我们所引入的函数G(B)仅是下列说法的一个简化了的表达式:个人可以被设想为拥有对可能的诸选择目标进行一致的并且具传递性的排列。甚至在原则上说,我们也只能通过观察个人在全部可能的目标之间所进行的选择,来确定他的G(B);如果从没有对个人提供过某种目标B,我们就永远不能计算出它相对于其他选择的排列位置。
一种特定的理论需要对G(B)形式做一些特定的说明。我们要考虑的一种非常特殊的理论如下:让选择目标B由收入I1的概率P1,收入I2的概率P2……,收入Ik的概率Pk组成,这样,这种特定的理论就可把G(B)写成如下的式子:
k
G(B)=∑
PiF(Ii)
i=I
这里F(I)仅是I的某种函数,换言之,这种特定理论包含着一种假设,即存在着函数F(I),它具有如下性质,在等式1中计算的G(B)可得到一种对各个可能选择的目标的正确排列。为了解释这一概念的意思,假设有像表4.1那样特定的B项和F项。这笔款项的数学期望为200,由∑PI式给出,这笔款项的G为18.75,由∑P·F(I)式给出。
表4.1
|
B |
I |
P |
F(I) |
|
P·F(I) |
100 |
1/4 |
10 |
|
2.5 |
200 |
1/2 |
20 |
|
10.0 |
300 |
1/4 |
25 |
|
6.25 |
|
|
|
强调一下G(B)=∑P·F(I)是一个很特别的假设是十分重要的。例如,考虑下列三笔款项:如表4.2中的B1,B2和B3。在B1的情况下,个人得失50美元的机会均等。在B2的情况下,个人得失100美元的机会均等。在B3的情况下,个人有25%得到100美元的机会,25%得到50美元的机会,25%的机会失掉50美元和25%的机会失掉100美元。假设我们知道个人在接受B1或B2的问题上无差异,也就是说,G(B1)和G(B2)相同,在上述特定理论的条件下,这意味着G(B3)等于G(B1)以及G(B2)。也就是,个人在B1、B2
和B3的选择上没有差异。
表4.2
|
B1 |
B2 |
B3 |
|
1/2(+50) |
1/2(+100) |
1/4(+100) |
|
1/2(-50) |
1/2(-100) |
1/4(+50) |
|
|
|
1/4(-50) |
|
|
|
1/4(-100) |
为了进一步讨论我们的特殊理论,我们可以从在某些收入之间选择的极端情况开始。在这种情况里,一笔款项B由一种单一收入比如说I组成,获得这种收入的概率为单位值,比如说P1=1,而获得任何其他收入的概率等于O。在这种情况下,G(B)=∑P1F(Ii)=F(I)。这就是为什么通常称F(I)为某笔收入的“效用”。我们在以后会有机会就它的用法提出一些问题,但在目前,我们可以把它作为一种方便的表达方式而予以接受。只要我们把自己限制在只讨论这些选择的范围里,关于F(I)我们所能了解的最多也就是它的导数的符号,也就是说,F是否随I增加或是减少。其结果像我们在前面对确定性的讨论一样,如果我们有使这些选择合理化的一个F(I),则具有正的一阶导数的F的任何函数也会是这样;也就是,如果F(I)能使选择合理化,只要f’>O,那么任何函数f(F[I])就也会这样。
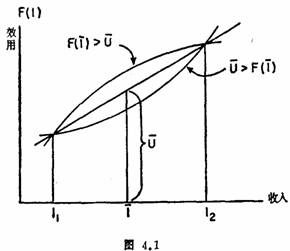
现在让我们介绍一下具有双重值的情况。考虑一下一个人面临着包括两项收入(I1和I2),其概率为P2,P2(P1+P2=1)的一级收入(一笔款项,B)的情形。预期的收入I=P1I1十P2I2。这项预期收入的效用等于F(I)。U,即预期效用等于P1F(I1)+P2F(I2)。如果联结收入的效用和收入的曲线呈下凹形,那么,预期的效用或U就小于预期收入的效用或F(I)。因此,肯定可以得到I的个人(如果任何特定的理论是正确的)就会喜欢这个结果而不是获得I1或I2的一次机会。然而,如果这条曲线呈上凸形,那么,预期效用或U就大于预期收入的效用F(I)。因此,个人就会选择可获得I1或I2的赌博,而不要可以获得I的确定性。上述情况在图4.1中用图形加以说明。
根据上面我们刚刚考虑的选择,我们将表明,如果我们接受G(B)=∑PF(I)的特定假设,则可能获得一种只是对范围和原点而言具有任意性的F(I)的函数。我们假设:如果I=0,那么F(I)=0;如果I=1,那么F(I)=1。我们现在已经消除了与范围和原点有关的不确定因素。现在我们要说明,我们如何确定I=2时的F(I)。如果给个人保证提供1美元(称此笔款项为B1)或者一种赌博,他有P1的机会一无所获或而有P1=1-P1的机会获得2美元(称此笔款项为B。)。让我们找出一个P1,使得个人在进行这两项选择时无差异,假若这个P1的值为1/4。既然个人在这两笔款项之间无差异,则G(B1)=G(B2)。由于G=∑PF(I),那么F(I)=P1F(O)+P2F(2)。由于我们已假设F(O)=O和F(I)=1,那么1=O+P2F(2)。由此可得F(2)=1/P2;或者,由于P2=3/4,F(2)=4/3,以相似的方式可以计算出所有其他收入的效用。我们能够唯一地导出F(2),因为我们就范围和原点作了任意的设想。更一般地讲,我们应该说如果任何F(I)可使选择合理化,则任何aF(I)+b的函数都会如此,只要a>O,后一个函数带来与范围和原点有关的不确定因素。
我们刚刚看到,我们能够根据关于个人从有限的几笔款项中,做出选择的知识,得出F(I),在每一种款项里都最多有两项可能的收入(在刚刚列举的例子里,例中的B1和B2加上其他由两项收入构成的组合,其中一项收入始终为O)。该F(I)除因原点和测度单位而引起的不确定问题外是唯一的。但是,由于我们能够从任何B计算出G(B),如果这种特定理论是有效的,则一旦我们知道了F(I),显然我们也就了解了个人如何排列可想象到的款项,因此可以说,这种特定理论具有十分真实的内容,也就是,它经得起反驳。
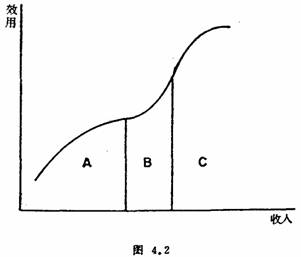
我们现在应该努力得到一个F(I)函数,这个函数应该是看起来能够对大多数观察到的现象做出说明。我们观察到,人们并不是有钱没处花,而且由此推知,人们将选择更多的收入而不是更少,这意味着F’(I)>O。我们知道,尽管有时根据保险统计计算,购买一项保险并不公平,人们还是要购买它。这就意味着对有些收入而言F”(I)
<0。另一方面,我们知道,人们都进行着赌博,包括购买保险的那些人。如果赌博与人们投保的风险完全一样,这一点就不能自圆其说,但赌搏不是这样。通常说来,他们购买的赌博如同买彩票,人们因此而获得巨奖的机会很渺茫,为了对这些现象做出合理说明,我们可以画一条象图4.2所示的曲线。在这个图上,A区为保险区域,比起巨大收入出现损失的很小机会来说,这里的人们宁愿选择收入上肯定会出现的一个小的损失。这是因为此处预期收入的效用大于预期效用,B区的存在说明了赌博的现象。由于它的存在,甚至A区的人们也可能会选择巨大所得的很小的机会,而不选择很小损失的很大的机会。这里的预期收入的效用少于预期效用。C区是必不可少的,可用它来说明有名的圣彼得堡悖论,它在彩票的设奖结构中也已不言自明。如果不是由于效用曲线在某些点上再次变成下凹形的这一事实,人们就会愿意花无数的钱去玩涉及圣彼得堡悖论的游戏。与此相同,如果效用曲线没有在某些点上再次变成下凹形的话,我们就应该想到彩票不是设几个奖,而是只设一个大奖。
也许应该就所有这些与可测效用问题的关系讲几句话。如果这个假设是正确的,那么,我们就可以建立起一个F(I)函数,该函数只是因范围和原点方面的原因而具有不确定的性质,然而,我们不需要把F(I)作为效用函数。确实,我们在前面把G(B)定义为效用函数。现在很明显,即使在我们的特定理论的条件下,如果一个G(B)可使选择合理化,则G(B)的任何函数都会如此,只要它不改变各选择的排列次序;也就是,如果你有一个G(B)=∑P·
F(I),则只要H’>o,,那么任何其他函数H[G(B)]=H[∑PF(I)]都会如此。
可以像下面这样更加概括地陈述我们的特定理论:有一组函数aF(I)+b,其中a为正数,b为任意数,使得一组函数H[G(B)]=H(∑P[aF(I)+b])。这里H’>0,产生一种个人对于不同收入的概率分市在偏好上的正确排列。也就是说,如果允许他在任何两个概率分布(比如说B1和B2)之间进行选择的话,他就会优先选择B1而不是B2,在B1与B2之间表现为无差异,或者优先选择B2而不是B1,这些都依H[G(B1)]>、=、<H[G(B2)]的情况而定。
很明显,起初的G(B)是最易使用的函数,但没有必要这样做。结果是,无法从“绝对”意义上把效用说成是“可测量”的。确实,在这种意义上,效用可否测量的问题到底有什么意义是大可怀疑的。
概率估值
为了导出 F(I)而假设的试验涉及到提出一些有关本题的赌博方式。对依那个函数而作的附加选择带有特定概率的推测需要能够确定附属于那些选择的概率。如何去做呢?
最适合我们效用分析的方法是由L.J.萨维奇充分发展了的“个人概率”方法,他是在布鲁诺·德·芬尼提工作的基础上创立这一方法的。这种方法是说,正象我们所能够设想的,个人在行动时,好象是把一个确定的效用——我们的F(I)函数的一般说法——赋予每一件有可能发生的事件,如果这一事件的确发生了的话,因此,我们也可以设想他在行动时似乎是把一个确定的概率赋予了每个这样的事件。人们假设这些“个人概率”服从概率数学的通常法则:也就是,被指定到一组相互排斥,且穷尽了各种情况的事件上(其中一个必须发生)的概率加总后等于一;被指定到两个互相独立事件上(两个都在发生)的联合概率是被指定到单个事件上的概率的积,等等。
原则上讲。这些个人概率是可以通过一系列假设的实验加以确定的,例如我们在推导F(I)时所引入的那种实验,只要此项概率试验在逻辑上先于那种效用试验,由于后者需要概率为已知,这些假设的概率试验能够为每个人都建立起概率的个人尺度,这些尺度可以用来决定他赋予任何事件的概率值,尽管它们是假设的。
实质上,试验的意图是,一旦特别的一组假设的事件发生,让个人选择他想如何得到报偿。例如,在抛出两枚硬币之前,让个人选择他愿意在(A)两枚都是正面时,还是在(B)出现其他结果(两枚都是反面,一个正面,一个反面)时获得一美元,像你可能猜测的,如果他选择当B发生时得到这一美元,这就意味着他认为B的概率要比A大,而且由于A和B是相互排斥和穷尽了各种情况的事件,故B的概率要大于一半。但是,当然没有任何东西来保证他会选择B。也许他检查了硬币,并发现两枚都是两面皆为正面的欺骗式硬币。注意,效用估值并没有进行。不管他选择A或B,奖赏都一样。他在决定可能发生的情况,在此情况下,他情愿获取其效用的相同的增量,也要注意,这里没有任何事情受到个人赋予他假设的、互相替代的事件的任何效用的影响。他可能会有一种特别想看到正面,而不是任何其他情况出现的热情,所以,如果A发生要比B发生使他可能从事件本身得到更多的效用。但是,他对于他要依此得到奖赏的终局情况的选择并不会影响什么结果发生,只是影响到,如果该结果发生,他是否能从一美元奖赏中获得新增的效用。
就这样的选择来做一个试验,直到你找到实验对象在引发奖励的结果方面无差异的一个选择。例如,假设(A)是一次一枚硬币抛掷的正面,(B)是那次抛掷的背面,并且实验对象表现为无差异的,一半时间选择A,一半选择B。然后把一半概率分配给A,上半给B,或一半分配给一次硬币抛掷的正面。在概率的语言里,他把硬币看作“公平”硬币。
确切说明了个人赋予其1/2概率的一个事件后,我们现在可以通过把那个事件作为引发奖赏的其中一个可供选择的基本事件,来确定他是否把其他事件的概率值估计为多于或少于一半。例如,如果(A)在某一天抛掷硬币出现正面,或(B)英国仍是议会民主制,他将宁愿从那一天起5年之后获得一个确定的奖赏。如果他选择B,我们知道,他把大于一半的概率分配给了那个可能性。
为了得到更加精确的个人概率预测,我们必须建立起一个更加精确的比较尺度。例如,提供奖赏给抛掷两枚硬币所获得的四种可能的结果中的任何一种:(A)两个正面;(B)两个反面;(C)正面和反面;(D)反面和正面。如果其结果引发奖赏对于实验对象是无差异的,我们就得到一组事件,对每个事件,这位实验对象都赋予1/4的概率,而且我们也还得到了两项假设的联合检验,一个假设是通常的数学概率法则适用于他的个人概率,另一个假设是他认为这两次抛掷是相互独立的。
原则上,这类试验会使人们有可能如愿以偿地得到一种较好的个人概率比较尺度,并由此而以任何所希望的精确程度确定他赋予任何假设事件的概率值。
每个人在行动时都象是已把一个个人概率值和一个效用值赋予了任何一个假设的事件,并以使预期效用最大化的方式,在提供给他的各种可能性中进行选择的这两个联合假设,现在是一个原则上未包括任何可观察到的因素的假设。
个人行动时好象他们已把个人概率分给所有可能事件的主张是关于行为的一种假设,不是个人心理的表述或关于个人对于一个事件,比如,英国议会民主的持续将赋予多大的概率这一问题将给予一个有意义答复的主张。如果讨论中的事件不很影响他的生活,或者尽管产生影响,不影响他可以控制的那部分行为,就没有理由说,他应该努力就这样一个问题下决心,并且他无疑将随便答复了事。另一方面,如果他的行为中一个重要的部分将有赖于英国的议会民主是否延续下去(用我们假设的试验的话说,如果那个结果所引发的奖赏或损失相当大),那就值得他花时间去构思一个确定的见解。
个人概率方法回避了有关文献里关于“客观”和“主观”概率的许多争论。个人概率方法能够与那个区别相联系的一种途径是,把那些所讨论的群体同意的概率集划分为“客观的”概率,而把那些他们不同意的概率划分为“主观的”概率。与经济学特别有关的一个例子是弗兰克·奈特强调的“风险”与“不确定性”的区别。实质上,“风险”与所谓客观概率相对应。“不确定性”与主观概率相对应。如果采用个人概率方法,这种区别就大大失去了说服力。 |